Sicherman Dice

History

In 1976 and 1977 I corresponded sporadically with Martin Gardner, author of the popular Mathematical Games column in the well-known monthly magazine Scientific American. In one letter, dated January 27, 1977, I depicted a hypothetical pair of dice with the spots rearranged. One die would bear the numbers 1–2–2–3–3–4; the other would bear 1–3–4–5–6–8. In spite of this unconventional arrangement of the spots, the pair of dice would produce values with the same probabilities as a pair of ordinary dice.

Gardner liked the idea and presented it in his column for February 1978, calling the dice Sicherman Dice—a name that has stuck. He mentioned that I had proved that the only sets of three or more dice that roll the same results as standard dice are standard dice, pairs of Sicherman Dice, and any combination of both.

In 1979 Sicherman Dice inspired two scholarly papers on the general subject of renumbered dice: Cyclotomic Polynomials and Nonstandard Dice by Joseph A. Gallian and David J. Rusin; and Renumbering of the Faces of Dice by Duane Broline. More papers on this subject appeared later. See the bibliography below for details.

Years later I was surprised to find Sicherman Dice for sale on the World-Wide Web. By 2009 Gamestation.net, a popular supplier of game equipment, offered them as a mixed pair. The 1–2–2–3–3–4 die was blue and the 1–3–4–5–6–8 die was green. In the rest of this article I will distinguish the dice by calling them blue and green.

At about the same time Grand Illusions, Ltd. brought out a white pair of Sicherman Dice with numerals instead of spots. Grand Illusions is still in business. Gamestation.net is not. Since then, other manufacturers have produced Sicherman Dice. See Suppliers below for a list of those known to me.

Physical Appearance

Arrangement of Spots

Sicherman Dice can have all the variations that conventional dice have. For example, they may be translucent or opaque; the dice and their spots can come in any colors; their corners may be square or rounded; their spots may be recessed or flush.

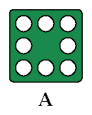
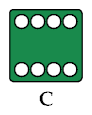
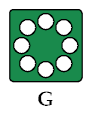
The arrangements of spots on the faces of Sicherman Dice usually match those on conventional dice, with the obvious exception of the 8. Here are some designs for the face with 8 spots:

Type A was used on the first pair of Sicherman Dice, which I had custom-made by a purveyor in Buffalo (George & Co.). Type D is the most efficient packing of the spots.

The arrangements of spots on the other faces can be varied, as in this set made by Legends of Ravenhall and colored by Alexandre Muñiz:

An advantage of varying the arrangements of spots is that it prevents Sicherman Dice from being mistaken for conventional dice.

Arrangement of Faces

On a traditional die, any pair of opposite faces adds up to seven. Sicherman Dice can be made so that the opposite faces of the blue die add up to five and the opposite faces of the green die add up to nine. With this arrangement, the blue die will have the two 2's on adjacent faces, and likewise the two 3's.

An alternative is to place the two 2's on opposite faces, and likewise the two 3's. The 1 and 4 will still lie on opposite faces.

So far as I know, all manufactured green dice obey the rule that opposite faces add up to nine.

Doubles

Doubles, or doublets, is a throw in which both dice show the same number. Doubles have special properties in some games. For example, in Backgammon a throw of doubles is played as four times the number rather than two times. In Craps, side bets may be laid on the chance of making a point with doubles.

Sicherman Dice do not preserve the probabilities of doubles. Indeed, some doubles cannot be thrown with Sicherman Dice: 2-2, 5-5, and 6-6.

Various methods have been proposed for defining throws of doubles with Sicherman Dice with the same probabilities as for standard dice. This entry at Alexandre Owen Muñiz's Puzzle Zapper Blog provides a good survey of such methods.

Software

Here is a Perl program that computes all sets of Sicherman-type dice for n-sided dice: sdice

Install Perl on your computer if necessary, then run the program like this:

$ sdice.pl 6 1 3 4 5 6 8 1 2 2 3 3 4 1 2 3 4 5 6 1 2 3 4 5 6 $

The first two printed lines are for Sicherman Dice; the second two are for standard dice. Specify a number n other than 6 for n-sided dice:

$ sdice.pl 8 1 2 2 3 3 4 4 5 1 3 5 5 7 7 9 11 1 2 2 3 5 6 6 7 1 3 3 5 5 7 7 9 1 2 3 3 4 4 5 6 1 2 5 5 6 6 9 10 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 $

Bibliography

Martin Gardner, Mathematical Games, Scientific American 238, 2 (1978-02), pp. 19–32.
Joseph A. Gallian and David J. Rusin, Cyclotomic Polynomials and Nonstandard Dice, Discrete Mathematics 27 (1979), pp. 245–259.
Duane Broline, Renumbering of the Faces of Dice, Mathematics Magazine 52, 5 (1979-05), pp. 312–315.
Lewis C. Robertson, Rae M. Shortt, and Stephen G. Landry, Dice with Fair Sums, American Mathematical Monthly 95 (1988), pp. 316–328.
Martin Gardner, Penrose Tiles to Trapdoor Ciphers, W. H. Freeman and Co., 1989, pp. 265–267.
B. W. Brunson and Randall J. Swift, Equally Likely Sums, Mathematical Spectrum 30, 2 (1997-08), pp. 34–36.
Randall J. Swift and Brian C. Fowler, Relabeling Dice, The College Mathematics Journal 30, 3 (1999), pp. 204–208.
Yutaka Nishiyama, Sicherman Dice: Equivalent Sums with a Pair of Dice, Osaka Keidai Ronshu 60, 2 (2009-07), pp. 185–192.
Wikipedia, Sicherman Dice.

Suppliers

This list is not warranted to be complete or up to date.

The Dice Shop.
Maths Gear. Made by Highland Games.
Noble Knight Games. Made by Legends of Ravenhall.
Trick-Dice.com. Formerly Highland Games.

Last revised 2023-03-15.

Col. George Sicherman [ HOME | MAIL ]