

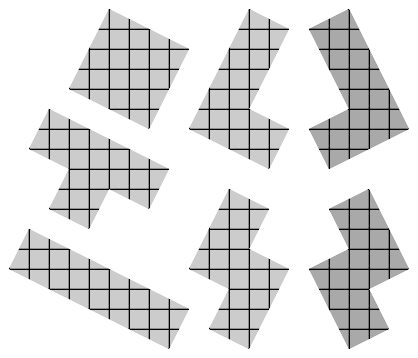
These pieces belong to a class of hybrid polyforms, or multi-polyforms, geometric shapes formed by joining two or more kinds of basic cells. For Shardinaires-9, these cells are the monomino and the monodom:

Doug Caine has named such polyforms polyshards, because they are generalized Shardinaires-9 pieces.
The diagram above shows seven tetrominoes. This is because two of the five have been flipped over so as to occupy different positions on the square grid. They have different solutions.
There are 12 different pentominoes:
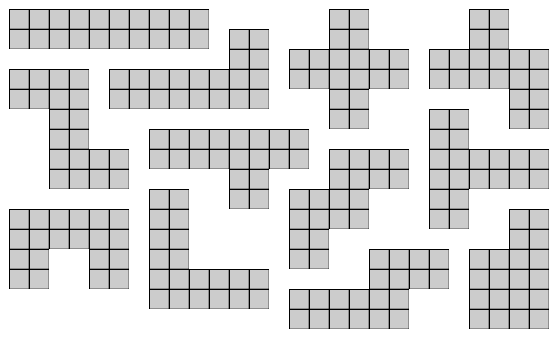
The first challenge for Shardinaires-9 is to arrange the 9 pieces to form every pentomino and every tetromino.
Another challenge is to form some polyominoes by using fewer than 9 pieces.

The instruction booklet for Shardinaires-9 is here. You can buy copies of Shardinaires-9 here.
In 2019, Kadon awarded Shardinaires-9 its GAPE (Gamepuzzles Annual Pentomino Excellence) Award.
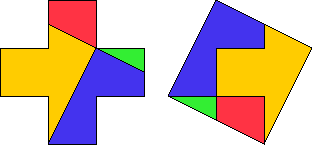
Donald sought a minimal set of pieces that could form every pentomino and every tetromino. The problem had been studied before, but not systematically. Donald used computer analysis to search for sets of pieces. The Loyd Polyominoes, a set of 8 pieces, were the result.
Acrylic sets of Loyd Polyominoes, made by Dave Janelle of Creative Crafthouse, were Donald's exchange gift at Gathering for Gardner 13 in 2018.

After Donald told me of his work, I joined the search, using software of my own. I found several sets of pieces that Donald had not found. Two of them had nine pieces, all different!
About a month after Gathering for Gardner 13, Kate Jones of Gamepuzzles.com found her gift set of Loyd Polyominoes. She and I discussed the set and its variants. In the end, Kate decided to manufacture one of my sets of 9 different pieces. She named it Shardinaires-9.
For months afterward, we developed new challenges for Shardinaires-9. When we had found enough, Kate wrote a booklet of them and began producing Shardinaires-9 for the retail market.