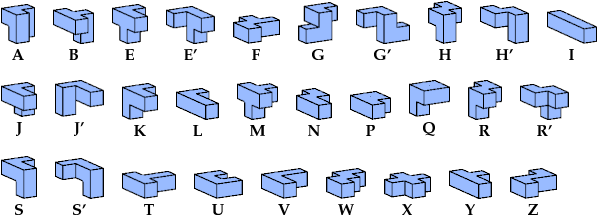

I indicate mirror images with a prime mark (′). For example, S′ denotes the mirror image of pentacube S.
All but two of the pentacubes, G and X, can tile a rectangular prism, or box. A box is odd if it has an odd number of cells. Such a box must have all its dimensions odd.
Here I show the smallest odd box known to be tilable with each pair of pentacubes, using at least one copy of each of the two pentacubes. If you find a solution smaller than one shown, or solve an unsolved case, please write.
See also Pentacube Pair Boxes.
| A | B | E | E′ | F | G | G′ | H | H′ | I | J | J′ | K | L | M | N | P | Q | R | R′ | S | S′ | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 25 | 9 | 15 | ? | 45 | 21 | 15 | 15 | 15 | 25 | 15 | 9 | 45 | ? | 15 | 15 | 15 | 15 | 21 | ? | 15 | 15 | |||||||
| B | 15 | 21 | 49 | 45 | 15 | 9 | 15 | 15 | 35 | 15 | 9 | 15 | 25 | 21 | 15 | 9 | 15 | 21 | 49 | 15 | 21 | ||||||||
| E | 15 | 15 | 15 | 21 | 15 | 15 | 9 | 9 | 9 | 9 | 9 | 9 | 15 | 9 | 9 | 9 | 15 | 9 | 15 | 15 | 9 | 9 | 9 | 21 | 15 | 15 | |||
| F | 21 | 15 | 9 | 15 | 15 | 7 | 21 | 15 | 9 | 15 | 21 | 15 | 21 | 9 | 9 | 21 | 63 | 5 | 9 | ||||||||||
| G | × | 45 | 45 | 27 | 15 | 9 | 21 | 15 | 65 | 21 | 9 | 45 | ? | ? | 33 | 21 | 27 | 15 | 15 | 33 | ? | 15 | 39 | ||||||
| H | 45 | 9 | 9 | 9 | 9 | 9 | 21 | 15 | 9 | 45 | 45 | 45 | 15 | 15 | 15 | 15 | 9 | 9 | 35 | 15 | 15 | ||||||||
| I | 15 | 21 | 3 | 15 | 15 | 3 | 9 | 15 | 21 | 9 | 9 | 7 | 9 | 9 | 7 | 9 | |||||||||||||
| J | 9 | 9 | 9 | 15 | 9 | 9 | 9 | 9 | 15 | 9 | 9 | 9 | 9 | 9 | 9 | 21 | 9 | 9 | |||||||||||
| K | 15 | 21 | 15 | 9 | 9 | 15 | 27 | 21 | 9 | 15 | 9 | 15 | 15 | 15 | |||||||||||||||
| L | 15 | 7 | 3 | 9 | 9 | 15 | 9 | 9 | 9 | 9 | 5 | 9 | 9 | ||||||||||||||||
| M | 21 | 9 | 15 | 35 | 15 | 21 | 9 | 21 | 21 | × | 15 | 21 | |||||||||||||||||
| N | 9 | 15 | 21 | 15 | 15 | 9 | 15 | 21 | 25 | 21 | 15 | ||||||||||||||||||
| P | 9 | 9 | 9 | 3 | 9 | 3 | 9 | 5 | 3 | 3 | |||||||||||||||||||
| Q | 45 | 9 | 9 | 15 | 9 | 9 | 15 | 15 | 9 | ||||||||||||||||||||
| R | 45 | 21 | 21 | 15 | 9 | 15 | 21 | 117 | 15 | 15 | |||||||||||||||||||
| S | 27 | 21 | 15 | 21 | 21 | 15 | 15 | 15 | |||||||||||||||||||||
| T | 9 | 15 | 21 | 55 | 9 | 25 | |||||||||||||||||||||||
| U | 9 | 21 | 3 | 11 | 9 | ||||||||||||||||||||||||
| V | 21 | 49 | 15 | 3 | |||||||||||||||||||||||||
| W | 57 | 15 | 15 | ||||||||||||||||||||||||||
| X | 5 | 63 | |||||||||||||||||||||||||||
| Y | 5 | ||||||||||||||||||||||||||||
| Z | |||||||||||||||||||||||||||||
M and X, colored like a 3D checkerboard, have four cells of one color and one of the other. Thus an odd number of M and X pentacubes have a net color imbalance that is an odd multiple of 3. Every odd box has a color imbalance of 1.
Last revised 2026-03-04.