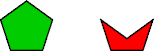
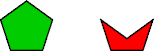
A polycrown is a plane figure formed by joining crowns edge to edge. Irmi Beyer introduced the terms crown and polycrown in 2025 in the Facebook group Mathematical Tiling and Tessellation. The crown is also known by names like dented pentagon, collapsed pentagon, and concave pentagon.
Livio Zucca analyzed crown tilings in 2003. You may see his results here at his site Remembrance of Software Past.
Yoshiaki Araki (荒木義明) has determined the convex spectrum of the crown pentagon. You may see his results on this page of Erich Friedman's Math Magic.
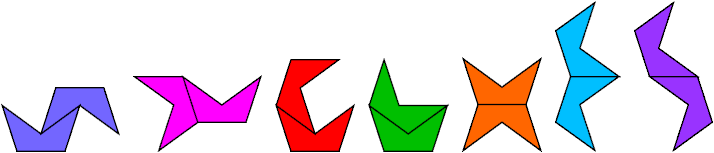
Here I show all polycrowns with 1, 2, or 3 cells. Irmi Beyer enumerated those with 1 and 2 cells.
See also
| Cells | Two-Sided | One-Sided |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 7 | 12 |
| 3 | 62 | 119 |
| 4 | 858 | 1 694 |
Rick Mabry enumerated the tetracrowns, subject to review.


Last revised 2025-07-25.