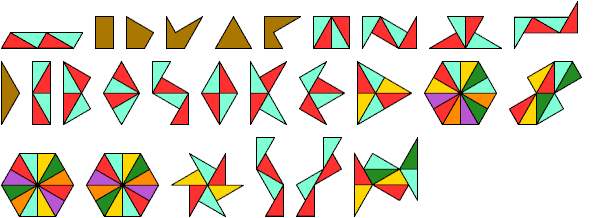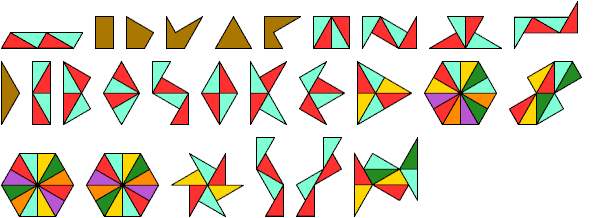Didrifter Integration

Introduction

A didrifter is a set of half cells in the polyiamond grid, joined along edges or at corners. It differs from a didrafter, whose cells are joined only at edges.

There are 27 didrifters. See this catalogue.

To integrate a vertex-connected polyform is to arrange copies of it without overlapping to form an edge-connected polyform. Here I show minimal known integrations for the didrifters.

The solutions shown are not necessarily uniquely minimal. Six of the didrifters are edge-connected (didrafters). They have trivial solutions, shown in gold.

Arbitrary Solutions

Here the integrated shapes may be extended polydrafters; that is, polydrafters whose drafter cells do not lie on a common polyiamond grid.

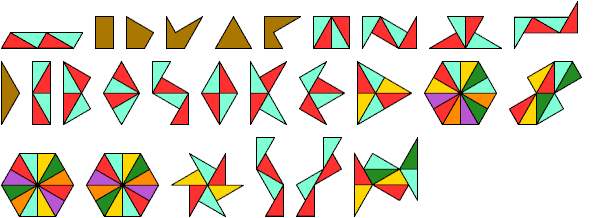
Conforming Variants

These solutions conform to the polyiamond grid. They have more tiles than the corresponding solutions in the previous section.

Last revised 2024-08-24.

Back to Polyform Exclusion, Equalization, Variegation, and Integration < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]