Pentahex Oddities
A pentahex oddity is a plane figure with binary
symmetry formed by joining an odd number of copies of a pentahex.
Here are the minimal known oddities for the pentahexes.
Please write if you find a smaller solution or solve an unsolved case.
See also
Trihex Oddities,
Tetrahex Oddities,
and
Hexahex Oddities.
Mike Reid
helped a lot with the pentahex oddities.
Click on the gray figures to expand them.
[ Basic Oddities
[ Holeless Variants
| Composite Solutions
| Nontrivial Variants
| Mirror-Symmetric Tilings ]
Basic Oddities
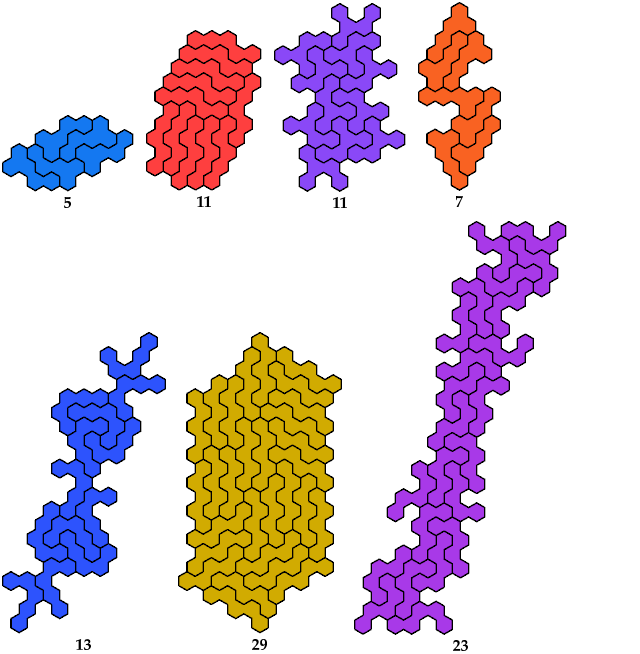
| Rowwise Bilateral
| Columnwise Bilateral
| Birotary | Double
Bilateral | Sextuple
Rotary | Full |
1

| 9

| 11

| 11

|
| |
1

| 9

|
|
|
| |
1

| 3

| 5

Mike Reid
| 5

Mike Reid
| 11

Mike Reid
| 11

Mike Reid
|
1

| 9

| 9

| 9

|
|
|
3

| 5
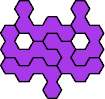
| 7

| 11

(after Mike Reid)
| 29

| 29
|
3

| 3

| 7
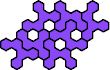
| 11

| 23

| 29

|
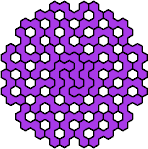
1

| 1

| 1

| 1

| 59
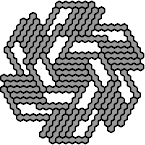
| 89

|
3

| 3

| 5

| 7

Mike Reid
| 29

|
|
3

| 3

| 5
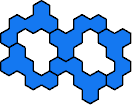
Mike Reid
| 9

| 17

| 35

|
3

| 3

| 5

Mike Reid
| 9

Mike Reid
| 17

| 23

|
3

| 3

| 3

| 5

Mike Reid
| 17

| 29

|
3

| 3

| 5

| 7

| 11

Mike Reid
| 11

Mike Reid
|
5

| 1

| 11
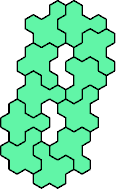
| 15

| 41

| 47

Mike Reid
|
3

| 5

| 7

| 11

| 23

| 35

|
7

| 3

| 1

| 7

|
|
|
9
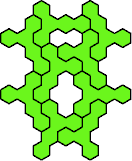
| 1

|
|
|
|
|
3

| 1

| 23

| 23

|
|
|
3

| 1

| 7

| 7

| 35

| 47

|
7

(squashed by Mike Reid)
| 1

| 9

| 9

| 53

| 53

|
1

| 1

| 1

| 1

| 101

|
|
3

| 5

| 7

| 9

| 17

| 17

|
5

| 5

| 7

| 15

| 17

| 17

|
Rowwise Bilateral
Columnwise Bilateral

Birotary
Double Bilateral
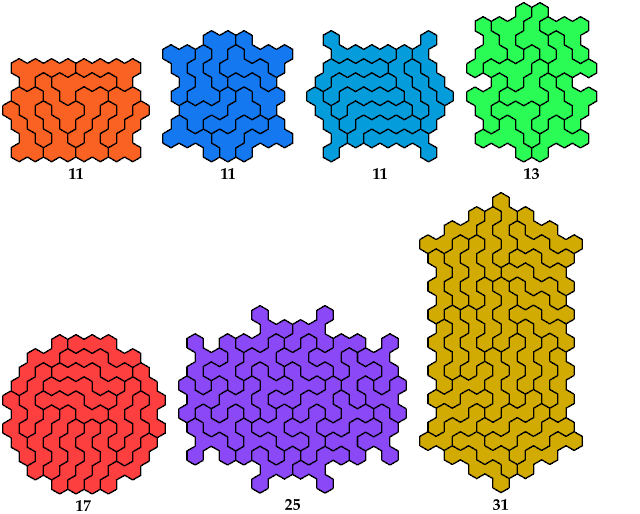
Sextuple Rotary

Full
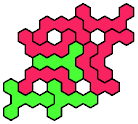
 Some pentahexes without oddities for certain symmetries
can be paired to form oddities.
Some pentahexes without oddities for certain symmetries
can be paired to form oddities.
Helmut Postl and Johann Schwenke found some of these
full-symmetric oddities.
Birotary
9 Tiles
Double Bilateral
11 Tiles

Sextuple Rotary
11 Tiles
17 Tiles

23 Tiles

35 Tiles
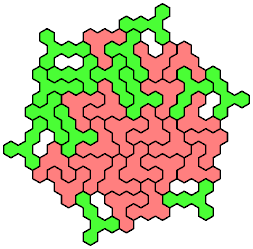
41 Tiles
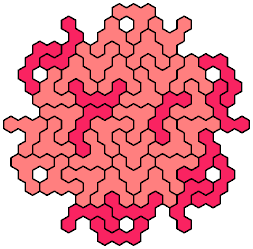
Full
11 Tiles
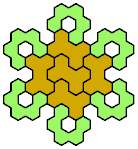
17 Tiles
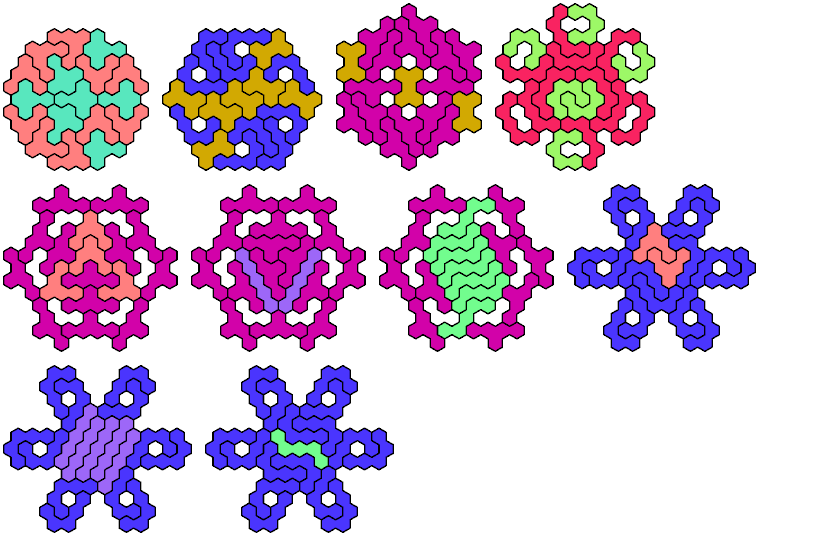
23 Tiles

29 Tiles
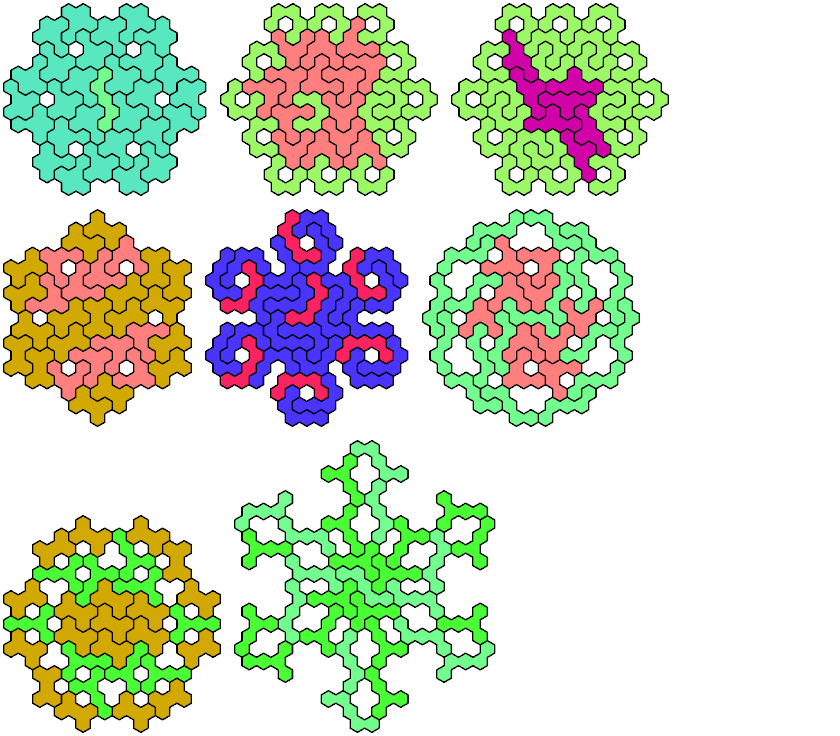
35 Tiles
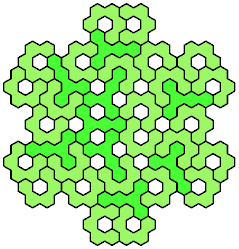
41 Tiles

53 Tiles
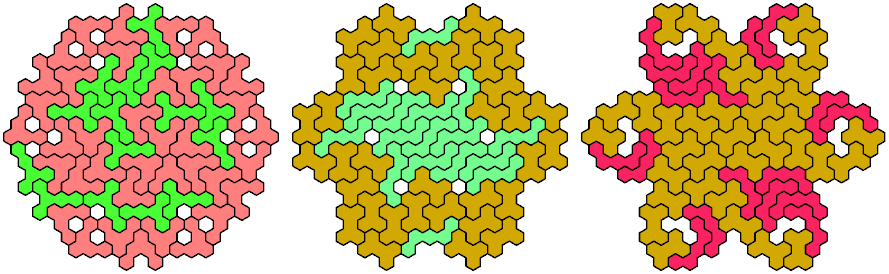
59 Tiles
 These tilings are irreducible and have more than one tile.
These tilings are irreducible and have more than one tile.
Rowwise Bilateral
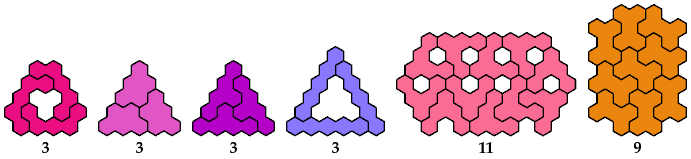
Columnwise Bilateral
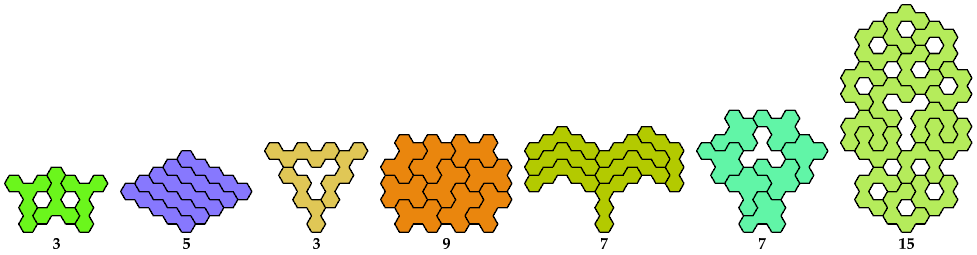
Birotary
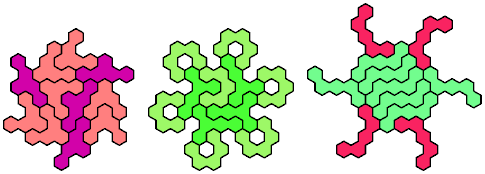
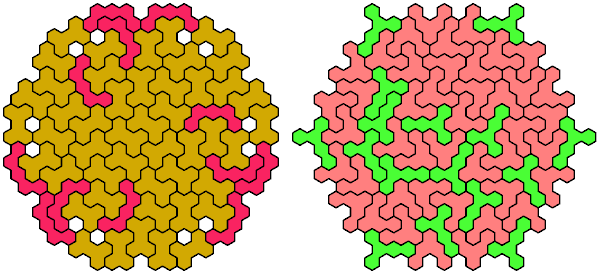
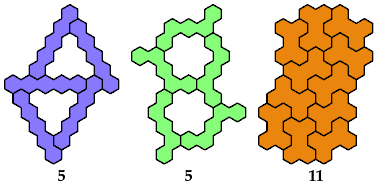 Mike Reid found that this full-symmetry oddity for the Q pentahex
can be tiled with vertical mirror symmetry!
Mike Reid found that this full-symmetry oddity for the Q pentahex
can be tiled with vertical mirror symmetry!
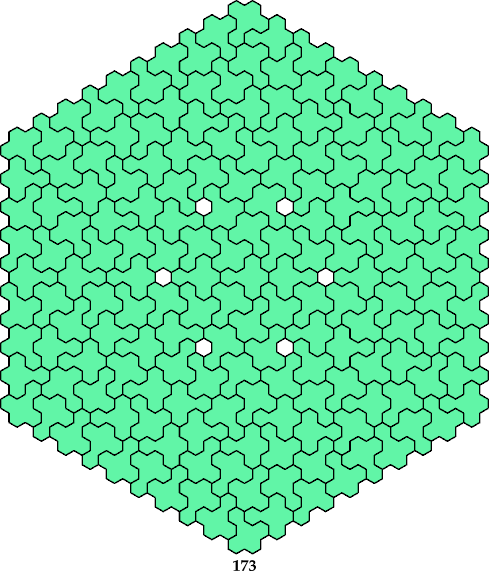
After Mike told me that a smaller solution probably existed,
I found this one:

Last revised 2024-10-29.
Back to
Polyform Oddities
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]











































































































































