
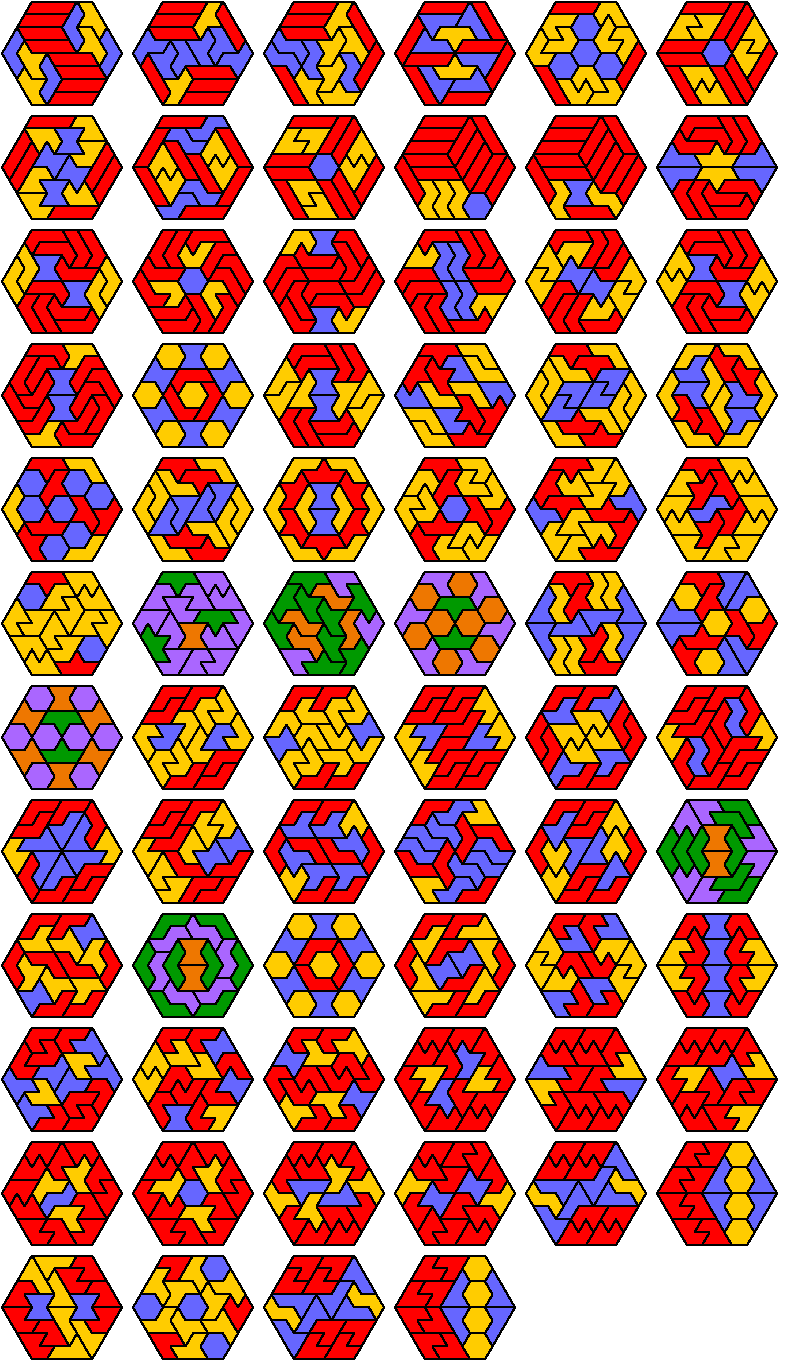
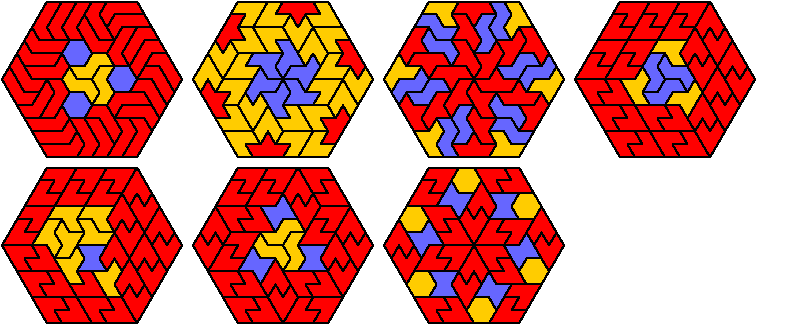
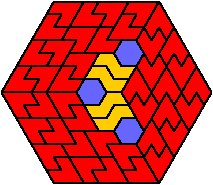
Here I show the smallest known regular hexagons that can be tiled by copies of three hexiamonds, using at least one of each. Tilings in green, violet, and orange are known to be unique for the hexagon shown. If you find a smaller solution or solve an unsolved case, please write.
| AEF 3 | AEH 6 | AEI ? | AEL 2 | AEO 3 | AEP 5 | AES 4 | AEU 3 | AEV 4 | AEX ? |
| AFH 4 | AFI 3 | AFL 2 | AFO 3 | AFP 4 | AFS 5 | AFU 4 | AFV 4 | AFX 4 | AHI 3 |
| AHL 3 | AHO 4 | AHP 5 | AHS 6 | AHU 4 | AHV 4 | AHX 6 | AIL 3 | AIO 4 | AIP 3 |
| AIS 4 | AIU 3 | AIV 3 | AIX ? | ALO 3 | ALP 3 | ALS 3 | ALU 2 | ALV 3 | ALX 4 |
| AOP 4 | AOS 7 | AOU 5 | AOV 3 | AOX 6 | APS 4 | APU 3 | APV 4 | APX 5 | ASU 5 |
| ASV 4 | ASX 6 | AUV 3 | AUX 4 | AVX 4 | EFH 4 | EFI 3 | EFL 3 | EFO 4 | EFP 3 |
| EFS 4 | EFU 3 | EFV 4 | EFX 4 | EHI 4 | EHL 3 | EHO 4 | EHP 5 | EHS 6 | EHU 3 |
| EHV 4 | EHX ? | EIL 3 | EIO 3 | EIP 4 | EIS 4 | EIU 3 | EIV 4 | EIX ? | ELO 2 |
| ELP 4 | ELS 3 | ELU 2 | ELV 3 | ELX 5 | EOP 4 | EOS ? | EOU 4 | EOV 4 | EOX 4 |
| EPS 4 | EPU 3 | EPV 4 | EPX 5 | ESU 3 | ESV 3 | ESX ? | EUV 3 | EUX 2 | EVX 4 |
| FHI 3 | FHL 3 | FHO 4 | FHP 4 | FHS 4 | FHU 3 | FHV 4 | FHX 4 | FIL 3 | FIO 4 |
| FIP 3 | FIS 3 | FIU 3 | FIV 3 | FIX 4 | FLO 3 | FLP 3 | FLS 4 | FLU 3 | FLV 3 |
| FLX 4 | FOP 4 | FOS 5 | FOU 3 | FOV 3 | FOX 5 | FPS 4 | FPU 3 | FPV 4 | FPX 4 |
| FSU 3 | FSV 4 | FSX 5 | FUV 4 | FUX 4 | FVX 4 | HIL 3 | HIO 3 | HIP 3 | HIS 3 |
| HIU 3 | HIV 3 | HIX 5 | HLO 3 | HLP 3 | HLS 3 | HLU 2 | HLV 3 | HLX 4 | HOP 3 |
| HOS 3 | HOU 3 | HOV 2 | HOX 5 | HPS 3 | HPU 3 | HPV 3 | HPX 5 | HSU 3 | HSV 2 |
| HSX ? | HUV 3 | HUX 4 | HVX 4 | ILO 3 | ILP 3 | ILS 3 | ILU 3 | ILV 3 | ILX 3 |
| IOP 3 | IOS 4 | IOU 4 | IOV 3 | IOX 3 | IPS 3 | IPU 3 | IPV 3 | IPX 3 | ISU 3 |
| ISV 3 | ISX 4 | IUV 3 | IUX 3 | IVX 3 | LOP 3 | LOS 6 | LOU 4 | LOV 3 | LOX 4 |
| LPS 3 | LPU 3 | LPV 3 | LPX 4 | LSU 3 | LSV 3 | LSX 5 | LUV 3 | LUX 4 | LVX 4 |
| OPS 3 | OPU 3 | OPV 3 | OPX 3 | OSU 5 | OSV 3 | OSX 5 | OUV 3 | OUX 5 | OVX 4 |
| PSU 3 | PSV 3 | PSX 3 | PUV 3 | PUX 3 | PVX 4 | SUV 3 | SUX 3 | SVX 4 | UVX 4 |



Last revised 2025-12-27.