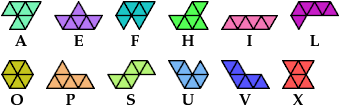
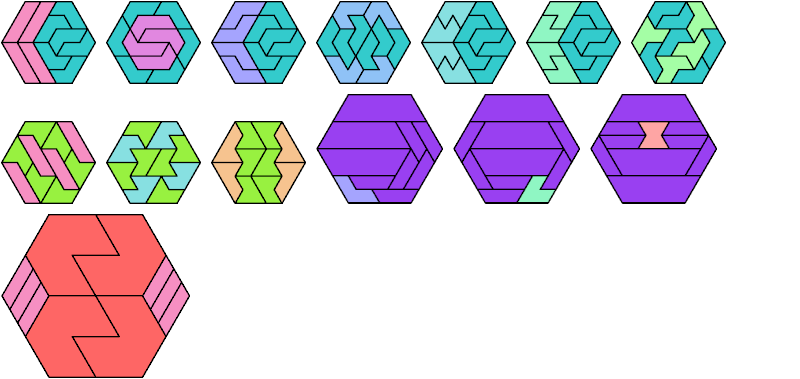
A hexiamond is a plane figure formed by joining six equal equilateral triangles edge to edge. There are 12 hexiamonds, independent of rotations and reflections:
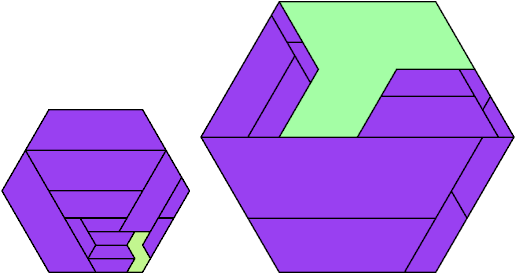
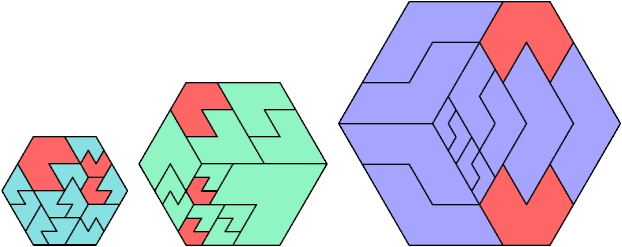
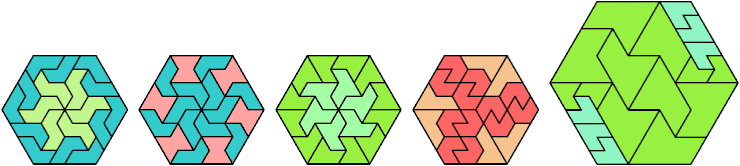
A scaled polyiamond is a polyiamond that may be scaled up by an integer factor.
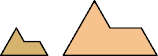
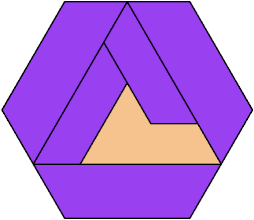
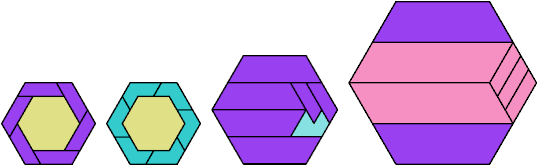
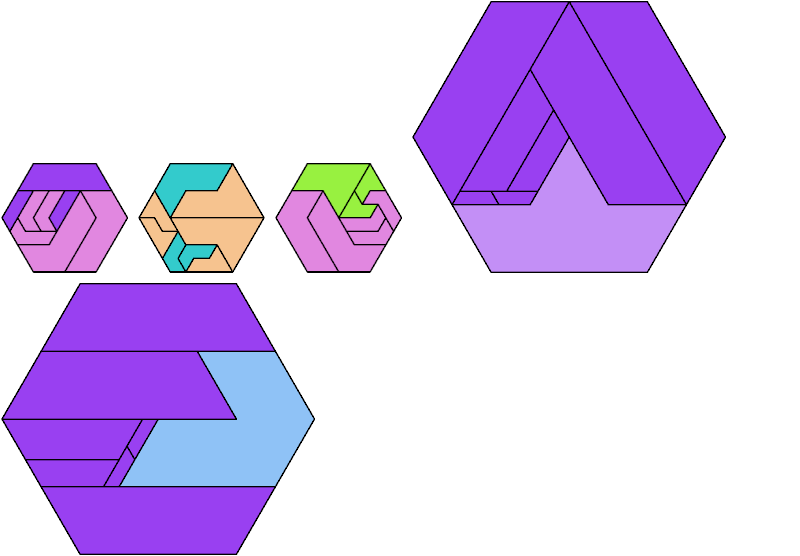
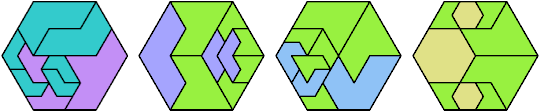
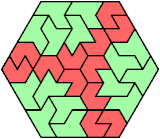
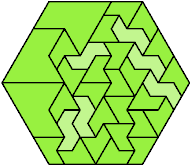
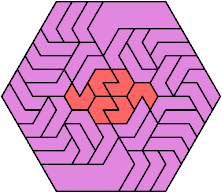
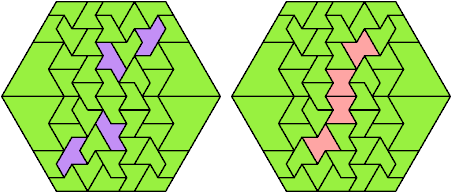
Here I show the fewest copies of two scalable hexiamonds that can tile some regular hexagon. If you find a smaller solution or solve an unsolved case, please write.
See also
| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 10 | 8 | 7 | 13 | 7 | 8 | 7 | 6 | 13 | 8 | 10 | 10 |
| J | 10 | 9 | 10 | 10 | 10 | 10 | 7 | 8 | 18 | 10 | 10 | 18 |
| Q | 20 | 46 | 10 | 18 | 10 | 8 | 9 | 10 | 33 | 9 | 9 | 46 |
| U | 14 | — | 14 | 27 | 10 | 44 | — | 18 | — | — | 14 | — |
Last revised 2025-03-31.