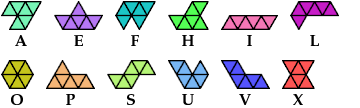

A scaled hexiamond is a hexiamond that may be scaled up by an integer factor.
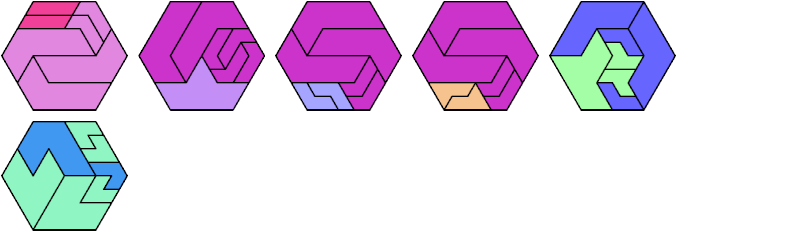
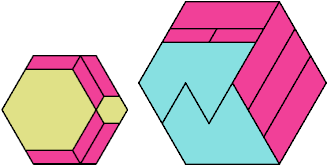
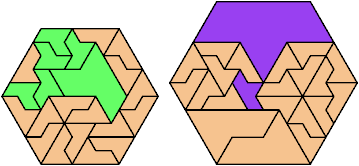
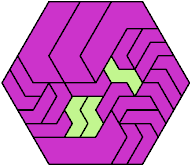
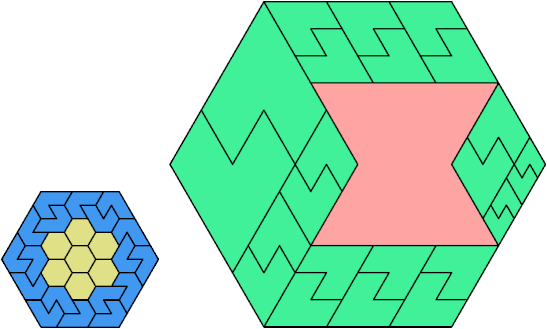
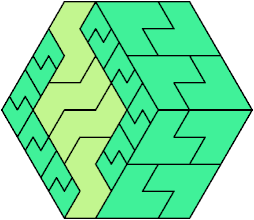
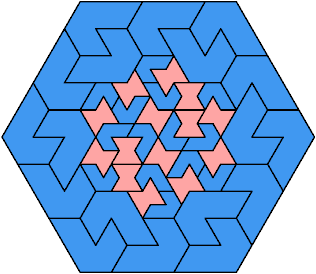
Here I show the fewest copies of two scalable hexiamonds that can tile some regular hexagon. If you find a smaller solution or solve an unsolved case, please write.
See also
| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 21 | 4 | 18 | 9 | 4 | 14 | 21 | 28 | 7 | 18 | 25 |
| E | 21 | * | 12 | — | 12 | 7 | 4 | 22 | — | 9 | 16 | — |
| F | 4 | 12 | * | 13 | 8 | 4 | 13 | 10 | 15 | 9 | 10 | 15 |
| H | 18 | — | 13 | * | 12 | 9 | 9 | 22 | — | 4 | 7 | — |
| I | 9 | 12 | 8 | 12 | * | 7 | 8 | 9 | 12 | 12 | 9 | 13 |
| L | 4 | 7 | 4 | 9 | 7 | * | 4 | 7 | 24 | 4 | 7 | 15 |
| O | 14 | 4 | 13 | 9 | 8 | 4 | * | 9 | — | 25 | 4 | 13 |
| P | 21 | 22 | 10 | 22 | 9 | 7 | 9 | * | 9 | 9 | 4 | 15 |
| S | 28 | — | 15 | — | 12 | 24 | — | 9 | * | 9 | 12 | — |
| U | 7 | 9 | 9 | 4 | 12 | 4 | 25 | 9 | 9 | * | 12 | 46 |
| V | 18 | 16 | 10 | 7 | 9 | 7 | 4 | 4 | 12 | 12 | * | 4 |
| X | 25 | — | 15 | — | 13 | 15 | 13 | 15 | — | 46 | 4 | * |

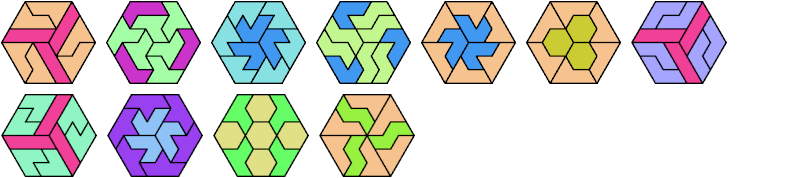
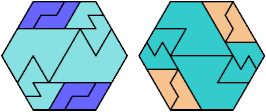
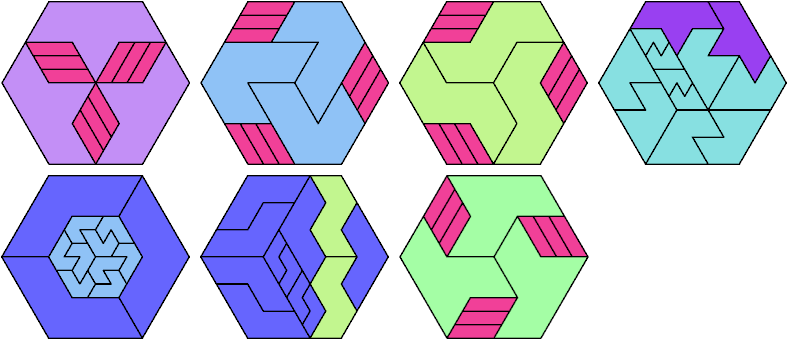
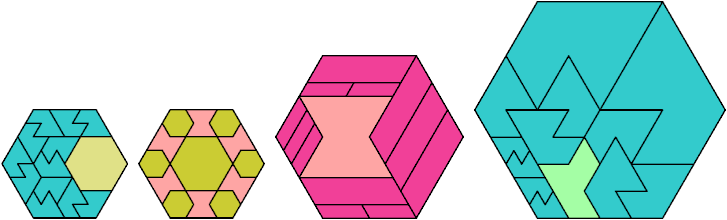
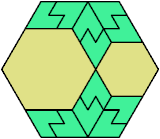
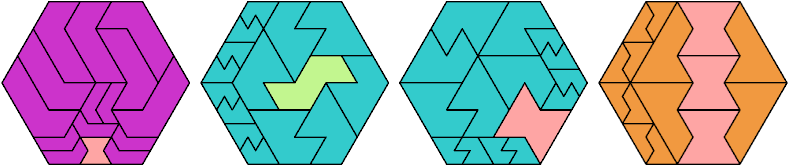

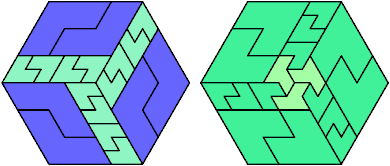
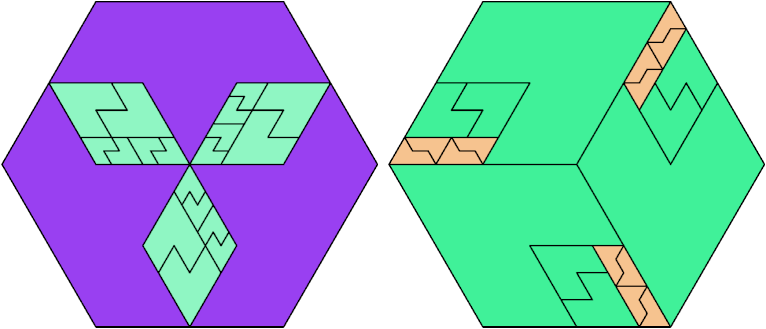
Last revised 2025-03-30.