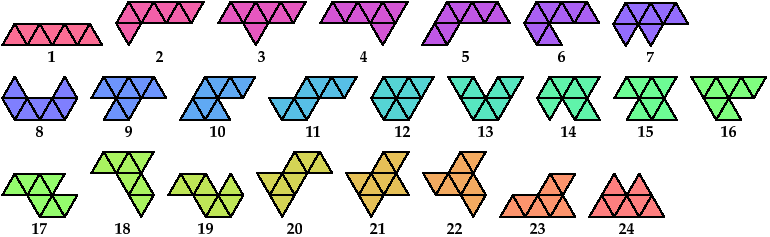
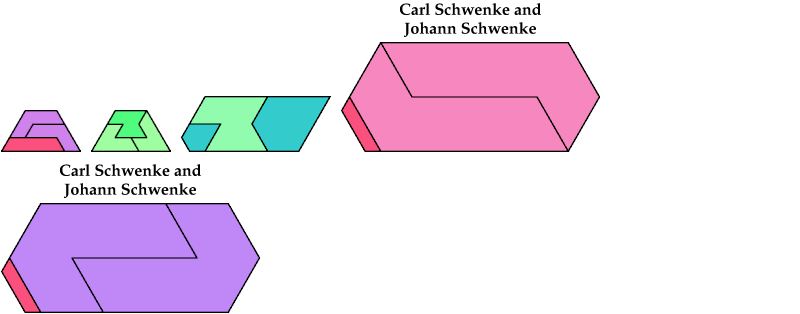
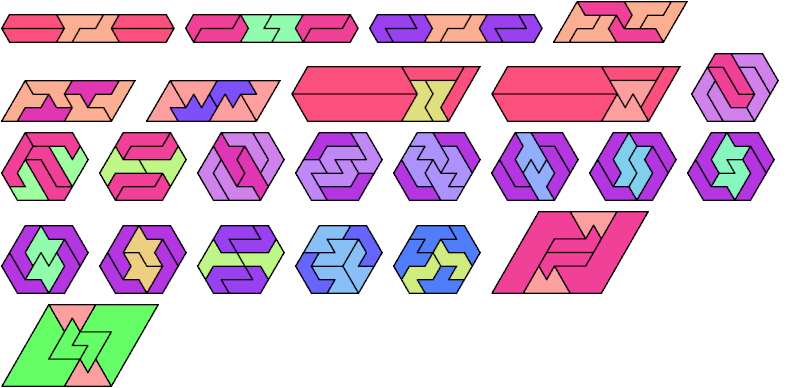
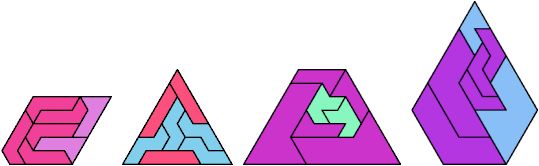
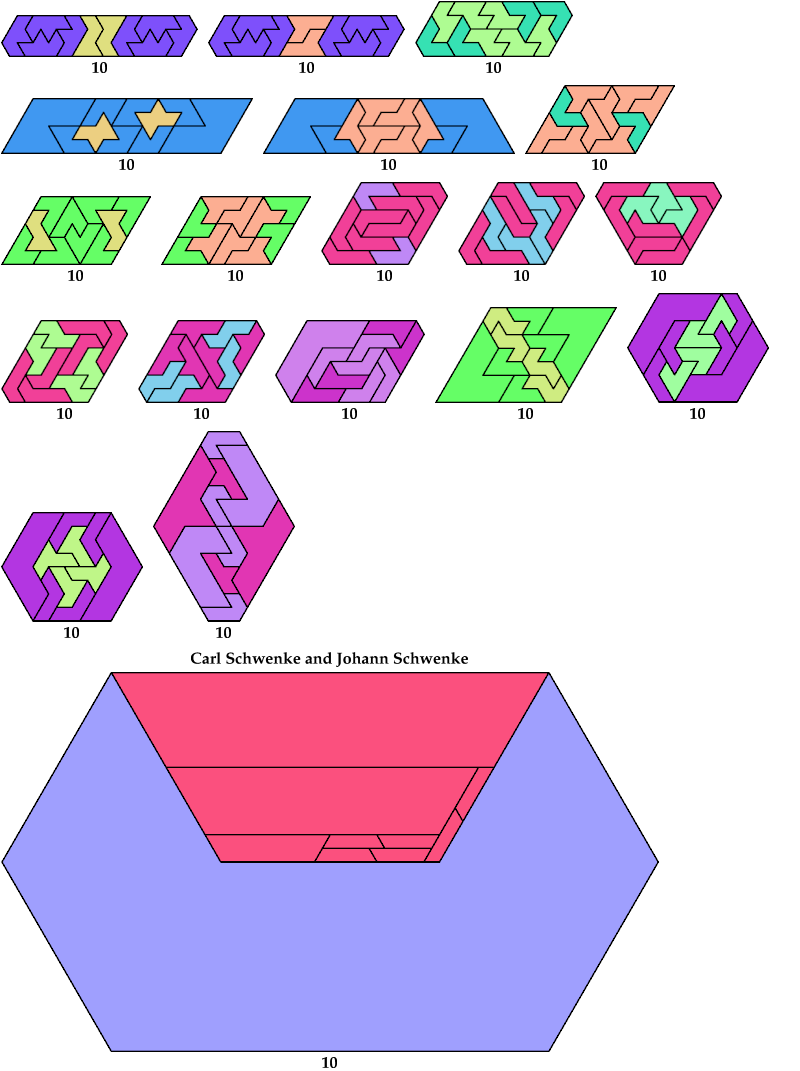
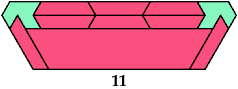
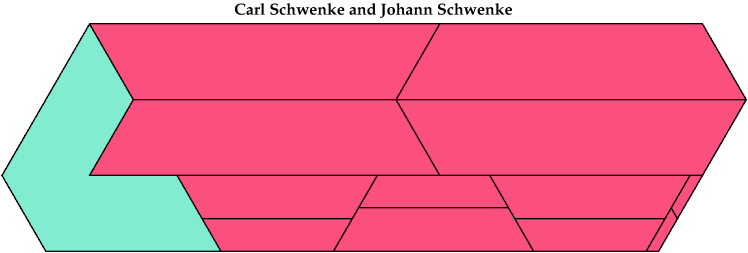
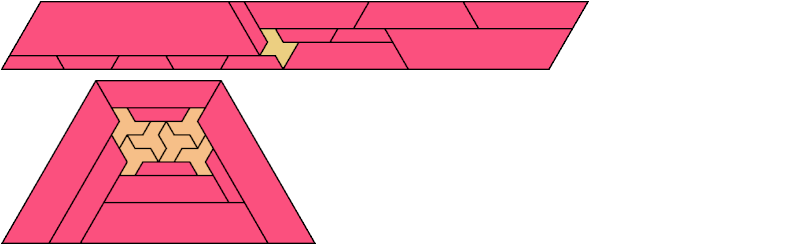
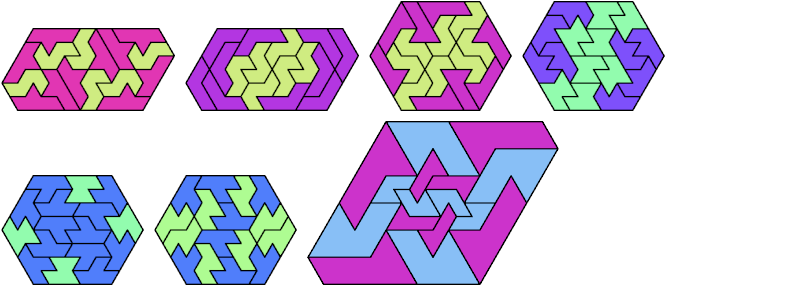
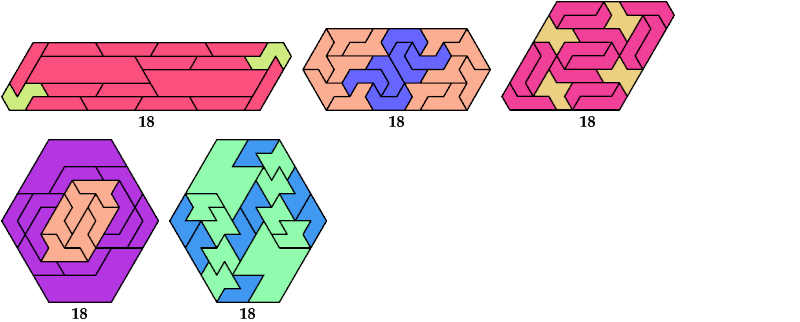
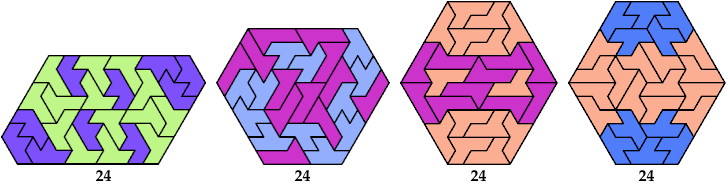
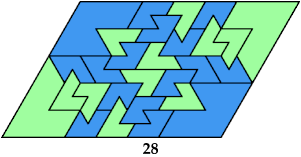
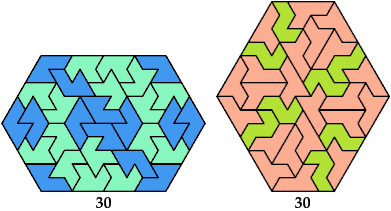
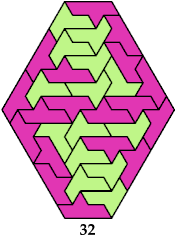
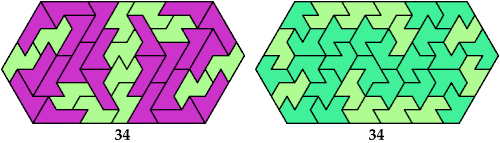
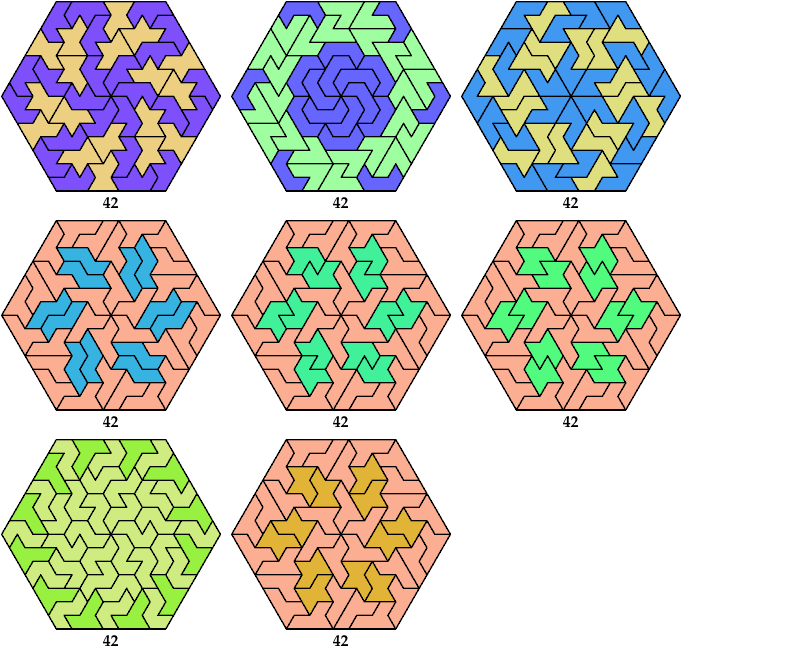
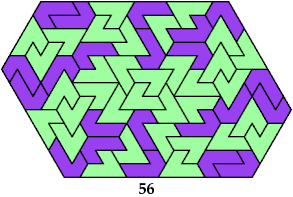
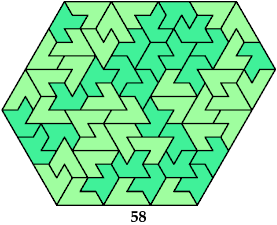
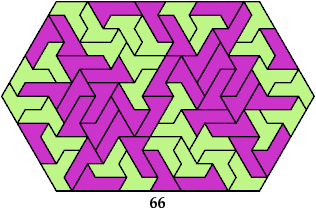
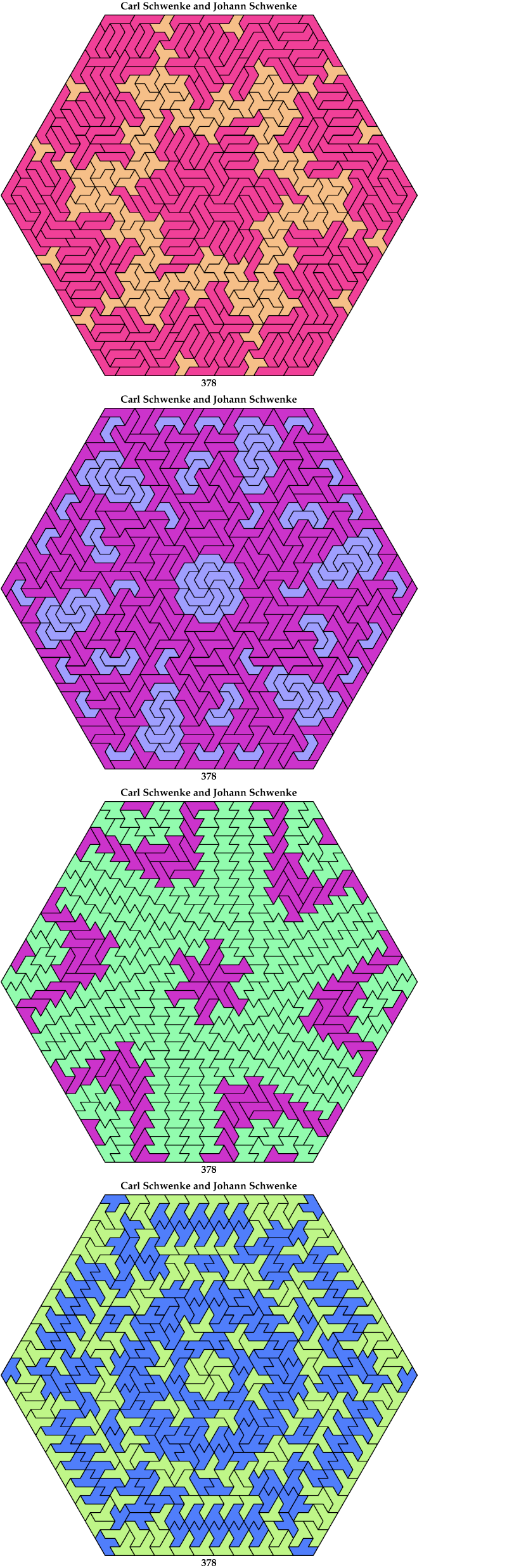
Convex Polygons From Pairs of Scaled Heptiamonds

Given two heptiamonds that may be scaled up, how few copies of them can be joined to form a convex shape? Such a shape must be a triangle, quadrilateral, pentagon, or hexagon.

Here I show minimal known convex polygons formed by pairs of scaled heptiamonds. If you find a smaller solution or solve an unsolved case, please write.

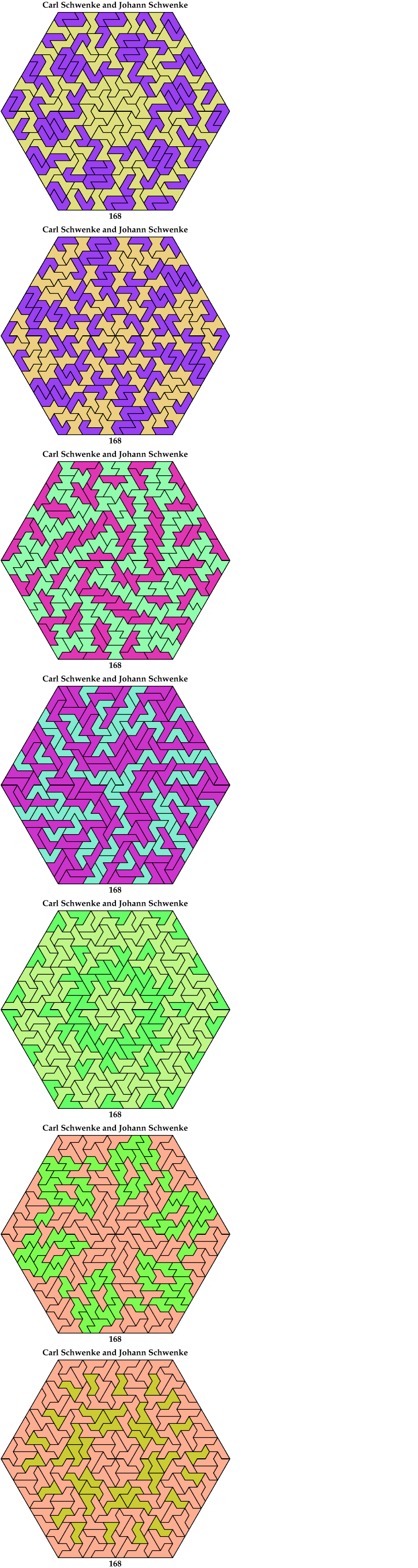
Carl Schwenke and Johann Schwenke found many new and improved solutions.

Heptiamond Numbers

Table

 123456789101112131415161718192021222324
1•312433410847213115484186151566
23•87610541451021410661064141837866
3128•—61014—44104241684143216———6—
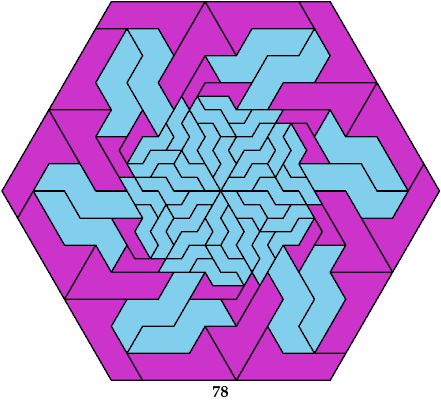
447—•1055378241678216873785346616———24—
536610•66—6764—66104101686—18—
63101056•4——4————45646—168168—62
74514564•—44—4—4162—2441042—106
8104—378———•—6—2—4—42—672————18—
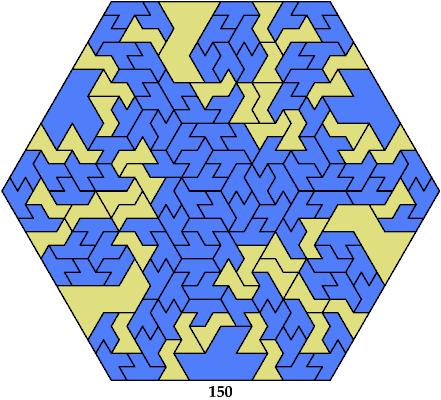
98144246—4—•4—4——164163786150——2454
104541674464•44—3018284——4210—10—
1171010786————4•—4——4——————42—
1222424—4244—•——3444—45—42
1313142168——————4—•44—10———4—10—
141110476—44—30——4•—5834—————4212
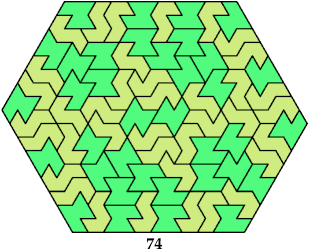
15561683786416—1618—34—•3——74———42—
164645105624242844—583•4168101012—106
17810143444——164—41034—4•—————168—
1846326610624672378——4———168—•42—————
19184161616—4—6—————7410—42•———30—
20614——816810—15042—4———10———•——168—
211518——616842——10—54——12————•—42—
2215378———————————————————•——
23666241861018241042410424210168—3016842—•—
2466———26—54——2—12—6———————•

2 Tiles

3 Tiles

4 Tiles

5 Tiles

6 Tiles

7 Tiles

8 Tiles

10 Tiles

11 Tiles

12 Tiles

13 Tiles

14 Tiles

15 Tiles

16 Tiles

18 Tiles

24 Tiles

28 Tiles

30 Tiles

32 Tiles

34 Tiles

42 Tiles

54 Tiles

56 Tiles

58 Tiles

66 Tiles

74 Tiles

78 Tiles

150 Tiles

168 Tiles

378 Tiles

672 Tiles

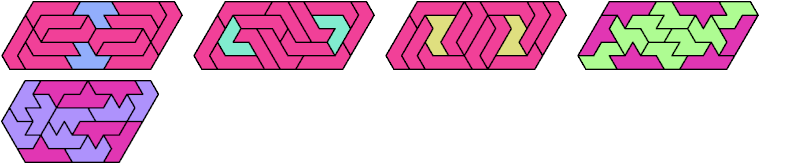
Last revised 2025-11-02.

Back to Convex Polygons from Pairs of Scaled Polyiamonds < Polyiamond and Polyming Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]