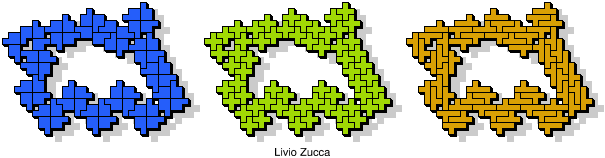
Here I combine Zucca's two problems and show compatibility figures for three pentominoes with an odd number of tiles!

His solution has 61 tiles! Smaller solutions have since been found. See the table below.
| 5F+5I+5L | 5F+5I+5N | 5F+5I+5P | 5F+5I+5T | 5F+5I+5U |
|---|---|---|---|---|
 23 | 
| 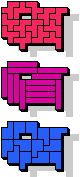 13 | 
| 
|
| 5F+5I+5V | 5F+5I+5W | 5F+5I+5X | 5F+5I+5Y | 5F+5I+5Z |

| 
| 
| 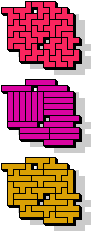 21 | 
|
| 5F+5L+5N | 5F+5L+5P | 5F+5L+5T | 5F+5L+5U | 5F+5L+5V |
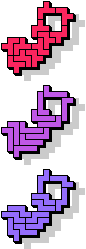 11 | 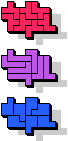 7 |  19 | 
| 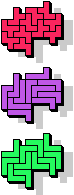 11 |
| 5F+5L+5W | 5F+5L+5X | 5F+5L+5Y | 5F+5L+5Z | 5F+5N+5P |
 15 | 
| 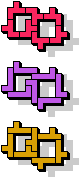 7 | 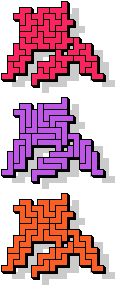 23 |  5 |
| 5F+5N+5T | 5F+5N+5U | 5F+5N+5V | 5F+5N+5W | 5F+5N+5X |
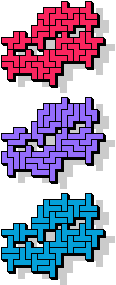 25 | 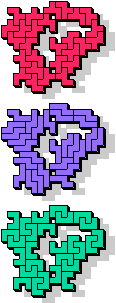 27 | 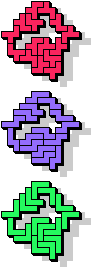 15 | 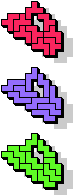 9 | 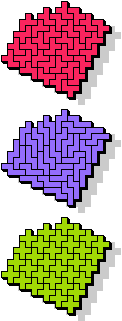 33 |
| 5F+5N+5Y | 5F+5N+5Z | 5F+5P+5T | 5F+5P+5U | 5F+5P+5V |
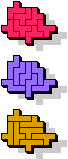 7 | 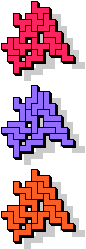 13 | 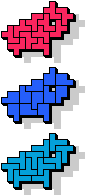 11 | 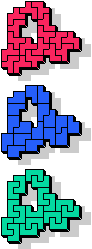 17 | 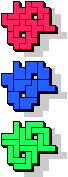 9 |
| 5F+5P+5W | 5F+5P+5X | 5F+5P+5Y | 5F+5P+5Z | 5F+5T+5U |
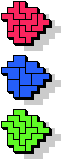 7 | 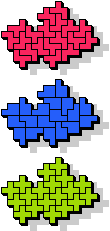 19 | 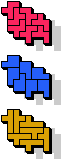 7 | 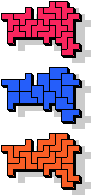 13 |  |
| 5F+5T+5V | 5F+5T+5W | 5F+5T+5X | 5F+5T+5Y | 5F+5T+5Z |

| 
| 
| 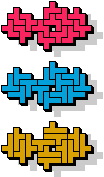 13 |  |
| 5F+5U+5V | 5F+5U+5W | 5F+5U+5X | 5F+5U+5Y | 5F+5U+5Z |

|  21 | 
| 
| 
|
| 5F+5V+5W | 5F+5V+5X | 5F+5V+5Y | 5F+5V+5Z | 5F+5W+5X |

| 
| 
| 
| 
|
| 5F+5W+5Y | 5F+5W+5Z | 5F+5X+5Y | 5F+5X+5Z | 5F+5Y+5Z |
 13 | 
|  17 | 
| 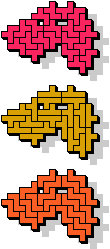 21 |
| 5I+5L+5N | 5I+5L+5P | 5I+5L+5T | 5I+5L+5U | 5I+5L+5V |

| 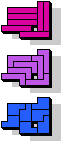 7 | 
| 
| 
|
| 5I+5L+5W | 5I+5L+5X | 5I+5L+5Y | 5I+5L+5Z | 5I+5N+5P |

| 
| 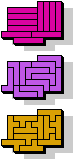 11 | 
| 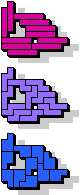 11 |
| 5I+5N+5T | 5I+5N+5U | 5I+5N+5V | 5I+5N+5W | 5I+5N+5X |

| 
| 
| 
| 
|
| 5I+5N+5Y | 5I+5N+5Z | 5I+5P+5T | 5I+5P+5U | 5I+5P+5V |
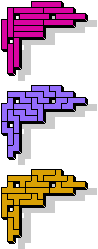 13 | 
| 
| 
| 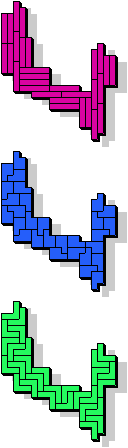 29 |
| 5I+5P+5W | 5I+5P+5X | 5I+5P+5Y | 5I+5P+5Z | 5I+5T+5U |
 17 | 
|  9 | 
| 
|
| 5I+5T+5V | 5I+5T+5W | 5I+5T+5X | 5I+5T+5Y | 5I+5T+5Z |

| 
| 
| 
| 
|
| 5I+5U+5V | 5I+5U+5W | 5I+5U+5X | 5I+5U+5Y | 5I+5U+5Z |

| 
| 
| 
| 
|
| 5I+5V+5W | 5I+5V+5X | 5I+5V+5Y | 5I+5V+5Z | 5I+5W+5X |

| 
| 
| 
| 
|
| 5I+5W+5Y | 5I+5W+5Z | 5I+5X+5Y | 5I+5X+5Z | 5I+5Y+5Z |
 29 | 
| 
| 
| 
|
| 5L+5N+5P | 5L+5N+5T | 5L+5N+5U | 5L+5N+5V | 5L+5N+5W |
 5 | 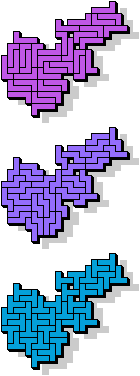 35 | 
| 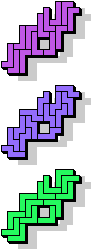 13 | 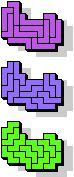 11 |
| 5L+5N+5X | 5L+5N+5Y | 5L+5N+5Z | 5L+5P+5T | 5L+5P+5U |

| 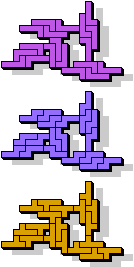 19 | 
| 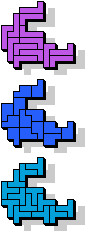 13 | 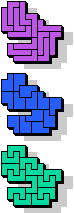 13 |
| 5L+5P+5V | 5L+5P+5W | 5L+5P+5X | 5L+5P+5Y | 5L+5P+5Z |
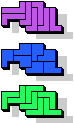 7 | 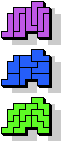 7 | 
| 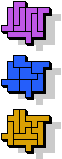 7 | 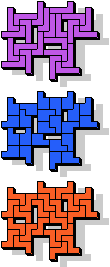 23 |
| 5L+5T+5U | 5L+5T+5V | 5L+5T+5W | 5L+5T+5X | 5L+5T+5Y |

| 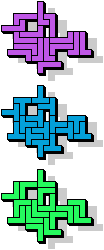 15 | 
| 
| 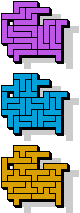 15 |
| 5L+5T+5Z | 5L+5U+5V | 5L+5U+5W | 5L+5U+5X | 5L+5U+5Y |

| 
| 
| 
| 
|
| 5L+5U+5Z | 5L+5V+5W | 5L+5V+5X | 5L+5V+5Y | 5L+5V+5Z |

| 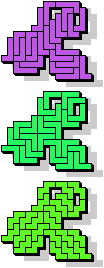 23 | 
| 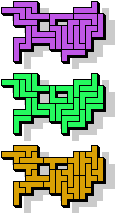 19 | 
|
| 5L+5W+5X | 5L+5W+5Y | 5L+5W+5Z | 5L+5X+5Y | 5L+5X+5Z |

|  13 | 
| 
| 
|
| 5L+5Y+5Z | 5N+5P+5T | 5N+5P+5U | 5N+5P+5V | 5N+5P+5W |
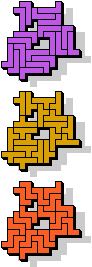 19 | 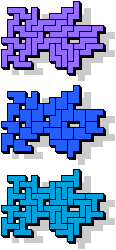 23 | 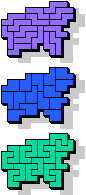 15 | 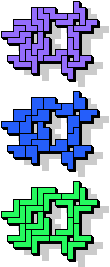 19 | 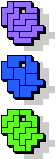 7 |
| 5N+5P+5X | 5N+5P+5Y | 5N+5P+5Z | 5N+5T+5U | 5N+5T+5V |
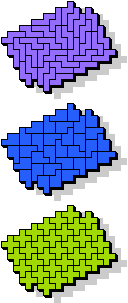 33 | 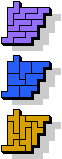 7 | 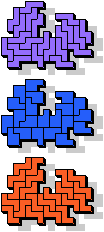 21 | 
| 
|
| 5N+5T+5W | 5N+5T+5X | 5N+5T+5Y | 5N+5T+5Z | 5N+5U+5V |

| 
| 
| 
| 
|
| 5N+5U+5W | 5N+5U+5X | 5N+5U+5Y | 5N+5U+5Z | 5N+5V+5W |

| 
| 
| 
| 
|
| 5N+5V+5X | 5N+5V+5Y | 5N+5V+5Z | 5N+5W+5X | 5N+5W+5Y |
 |

| 
|  |

|
| 5N+5W+5Z | 5N+5X+5Y | 5N+5X+5Z | 5N+5Y+5Z | 5P+5T+5U |

| 
|  |
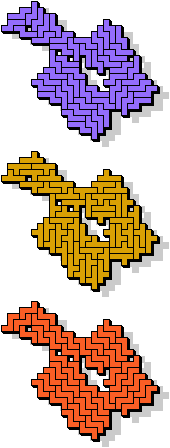 51 | 
|
| 5P+5T+5V | 5P+5T+5W | 5P+5T+5X | 5P+5T+5Y | 5P+5T+5Z |
 15 | 
| 
| 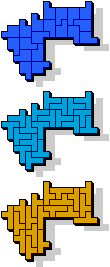 19 | 
|
| 5P+5U+5V | 5P+5U+5W | 5P+5U+5X | 5P+5U+5Y | 5P+5U+5Z |

| 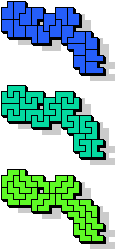 19 |  |

| 
|
| 5P+5V+5W | 5P+5V+5X | 5P+5V+5Y | 5P+5V+5Z | 5P+5W+5X |
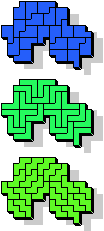 21 |  |
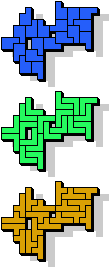 19 | 
| 
|
| 5P+5W+5Y | 5P+5W+5Z | 5P+5X+5Y | 5P+5X+5Z | 5P+5Y+5Z |
 11 |  15 |  29 |  |
 11 |
| 5T+5U+5V | 5T+5U+5W | 5T+5U+5X | 5T+5U+5Y | 5T+5U+5Z |

| 
| 
| 
| 
|
| 5T+5V+5W | 5T+5V+5X | 5T+5V+5Y | 5T+5V+5Z | 5T+5W+5X |

| 
| 
| 
| 
|
| 5T+5W+5Y | 5T+5W+5Z | 5T+5X+5Y | 5T+5X+5Z | 5T+5Y+5Z |

| 
| 
| 
| 
|
| 5U+5V+5W | 5U+5V+5X | 5U+5V+5Y | 5U+5V+5Z | 5U+5W+5X |

| 
| 
| 
| 
|
| 5U+5W+5Y | 5U+5W+5Z | 5U+5X+5Y | 5U+5X+5Z | 5U+5Y+5Z |

| 
| 
| 
| 
|
| 5V+5W+5X | 5V+5W+5Y | 5V+5W+5Z | 5V+5X+5Y | 5V+5X+5Z |
 |

| 
|  |

|
| 5V+5Y+5Z | 5W+5X+5Y | 5W+5X+5Z | 5W+5Y+5Z | 5X+5Y+5Z |

|  |
 |

|  |
Last updated 2017-08-26.