
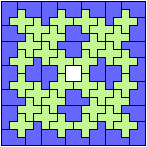
The January 2008 issue of Erich Friedman's Math Magic defined a frame as a square polyomino with a centered square hole. The problem was to find the frame with least area that could be tiled with a given polyomino.
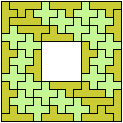
Here I study the related problem of finding the smallest frame that can be tiled with two pentominoes. Thanks to Joyce Michel for suggesting this problem.
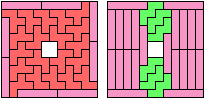
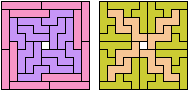
Bryce Herdt solved a balanced variant.
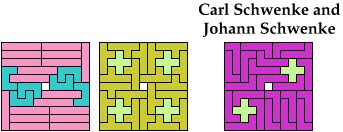
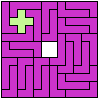
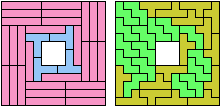
Carl Schwenke and Johann Schwenke improved on
some of my solutions.
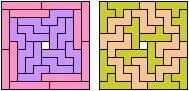
They also noticed that my balanced variant
for pentominoes I and Z
had fewer tiles than my general solution!

| F | I | L | N | P | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | • | 28 | 8 | — | 12 | — | 16 | 12 | — | — | 8 | — |
| I | 28 | • | 8 | 12 | 8 | 8 | 24 | 8 | 28 | ? | 8 | 64 |
| L | 8 | 8 | • | 8 | 8 | 12 | 12 | 8 | 12 | 24 | 8 | 16 |
| N | — | 12 | 8 | • | 8 | 8 | 16 | 12 | — | — | 8 | — |
| P | 12 | 8 | 8 | 8 | • | 12 | 8 | 12 | 12 | 12 | 8 | 12 |
| T | — | 8 | 12 | 8 | 12 | • | 12 | — | 12 | — | 16 | — |
| U | 16 | 24 | 12 | 16 | 8 | 12 | • | 88 | — | 12 | 12 | — |
| V | 12 | 8 | 8 | 12 | 12 | — | 88 | • | 64 | — | 8 | 8 |
| W | — | 28 | 12 | — | 12 | 12 | — | 64 | • | — | 12 | — |
| X | — | ? | 24 | — | 12 | — | 12 | — | — | • | 24 | — |
| Y | 8 | 8 | 8 | 8 | 8 | 16 | 12 | 8 | 12 | 24 | • | 16 |
| Z | — | 64 | 16 | — | 12 | — | — | 8 | — | — | 16 | • |



















Last revised 2024-02-27.