Isolated Pentomino Pair Rectangles

Introduction

Here are the smallest known rectangles that can be formed by any pair of pentominoes, using at least one of each, and isolating the copies of one. I use Andrew Bayly's definition of isolation: the isolated copies may not touch even at corners.

If you find a smaller solution, or solve an unsolved case, please write.

Andrew Bayly found some new and improved solutions.

See also

  • Isolated Hexomino Pair Rectangles, at Andrew's Blog

    • 3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    7 Tiles

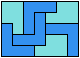
    8 Tiles

    9 Tiles

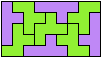
    10 Tiles

    11 Tiles

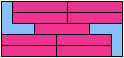
    12 Tiles

    14 Tiles

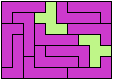
    16 Tiles

    18 Tiles

    30 Tiles

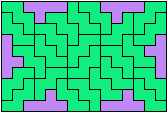
    32 Tiles

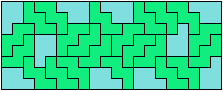
    33 Tiles

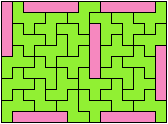
    42 Tiles

    55 Tiles

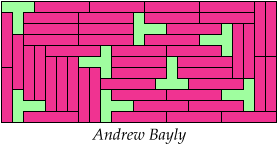
    65 Tiles

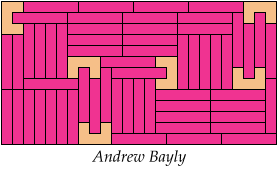
    66 Tiles

    72 Tiles

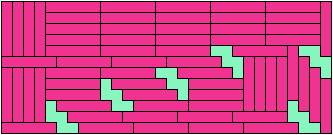
    76 Tiles

    77 Tiles

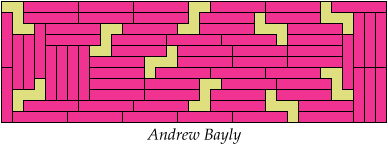
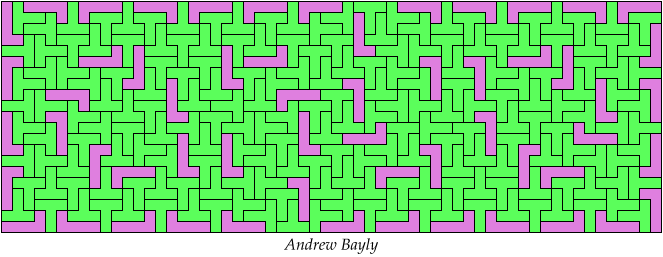
    252 Tiles

    Last revised 2025-07-24.

    Back to Polyomino and Polyking Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]