

A pentapent is a plane figure formed by joining 5 equal regular pentagons edge to edge:
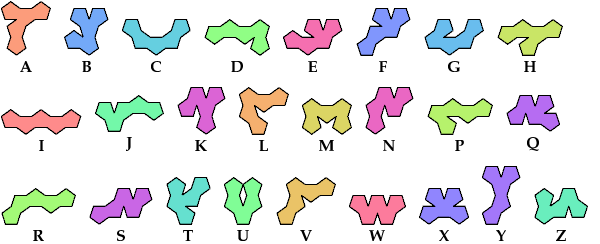
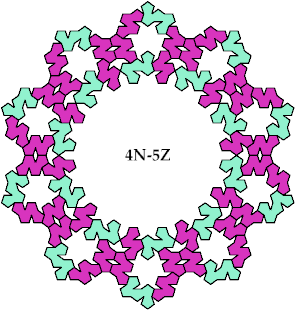
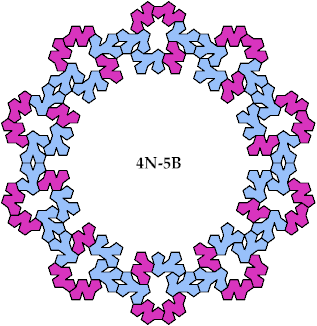
A Baiocchi figure is a figure formed by joining copies of a polyform and having the maximal symmetry for the polyform's class. For polypents, that means the symmetry of a regular decagon, or 10-way rotary with reflection.
Baiocchi Figures may also be defined for sets of tiles. For each combination of one tetrapent and one pentapent, I show here a Baiocchi Figure with minimal area. If you find a smaller solution, please write.
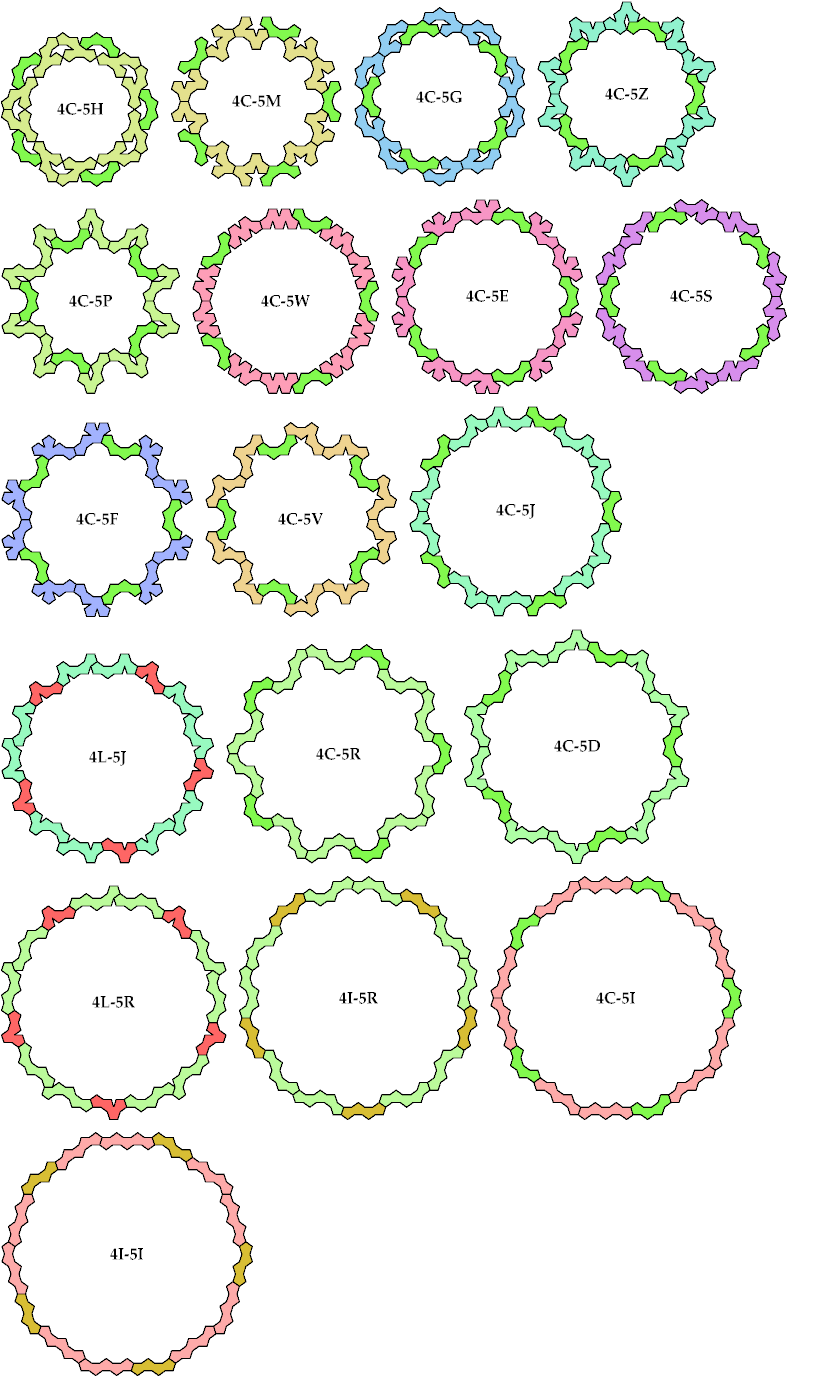

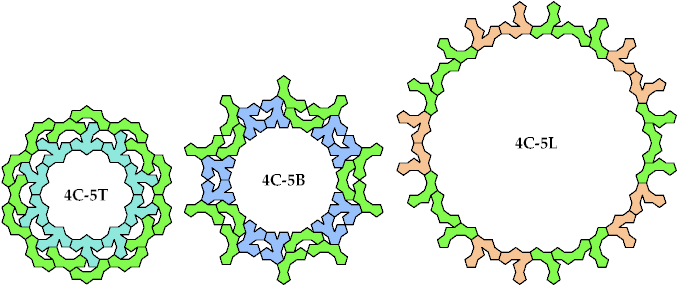
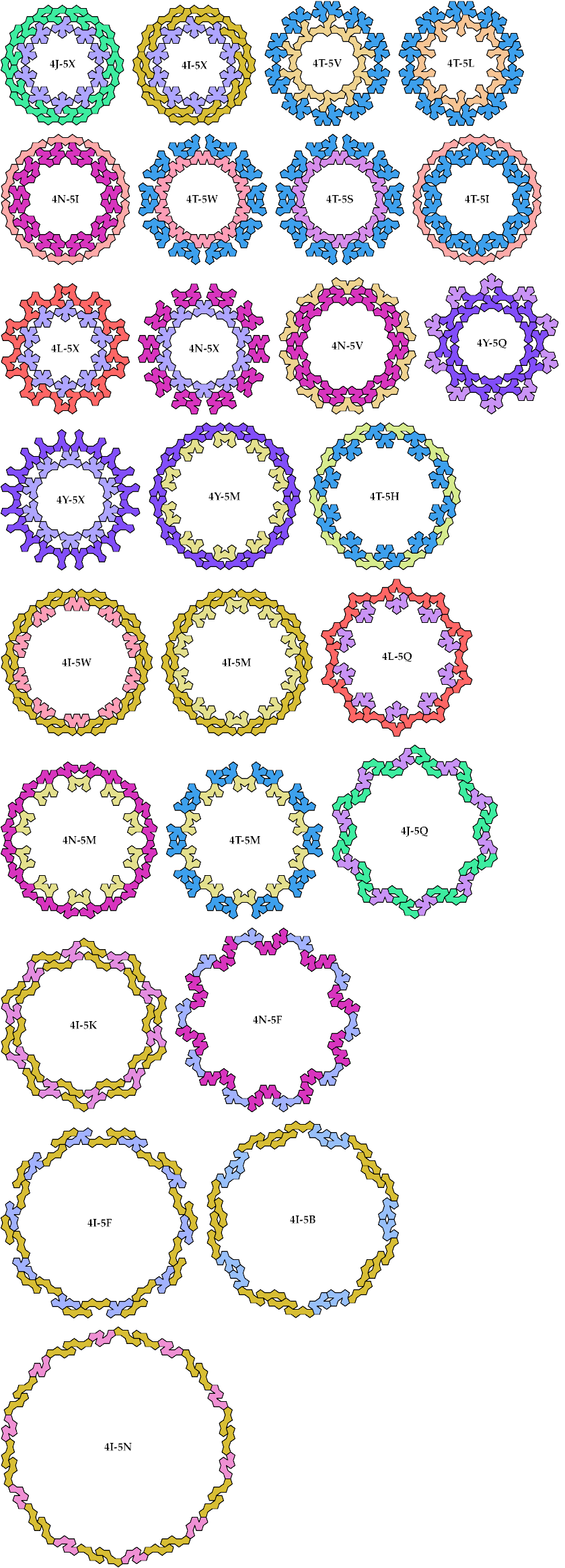
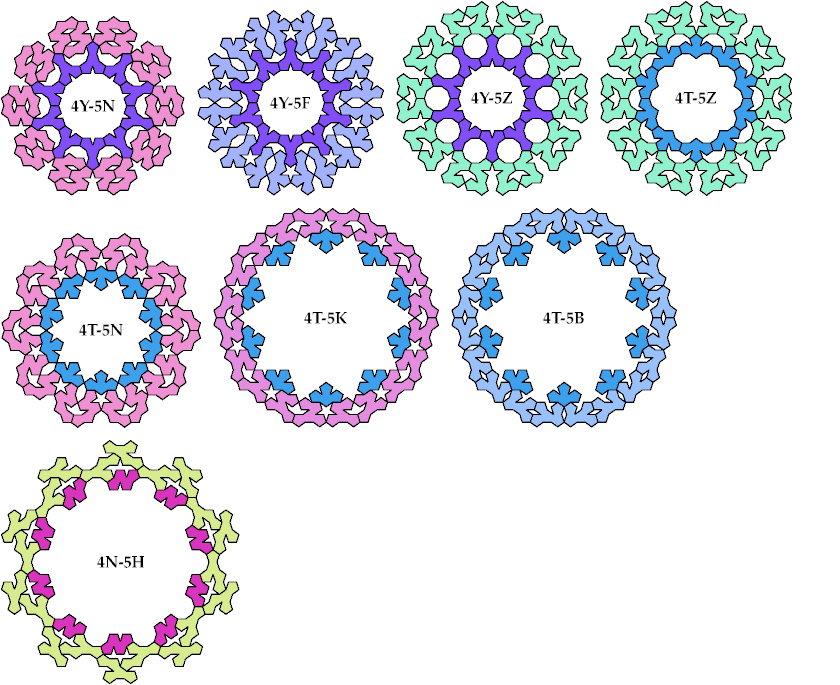
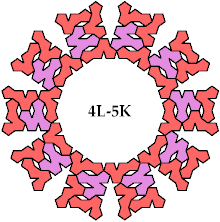
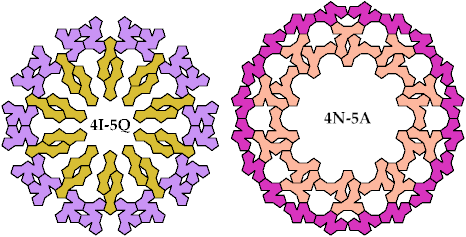
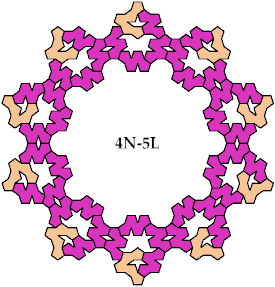

Last revised 2024-09-18.