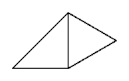

Its interior angles are 45°, 105°, 60°, and 150°. It was first studied by Dr. Karl Scherer.
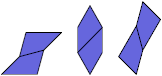
A discherer is a polyform formed by joining two Scherer quadrangles at equal edges. There are 14 discherers, identifying mirror images:

A Baiocchi Figure for a polyform P is a polyform made by joining copies of P and having the maximum symmetry for that class of polyforms. For polyscherers this is 12-fold rotary symmetry with reflection.
Here I show a minimal known Baiocchi Figure, if any, for each discherer.
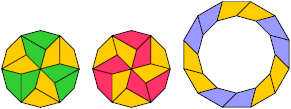
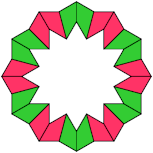

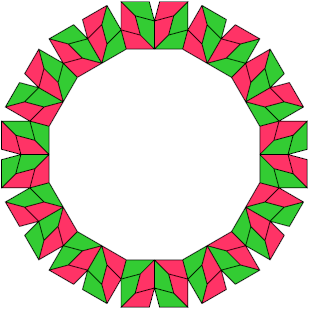

Last revised 2025-10-15.