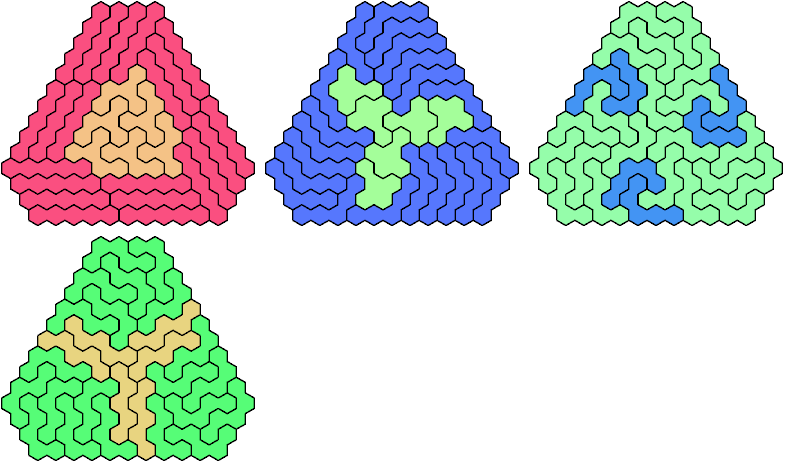
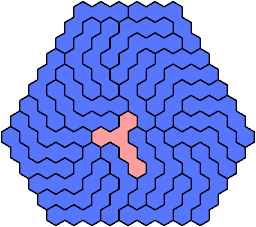
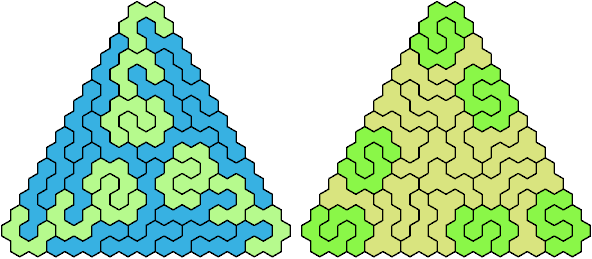
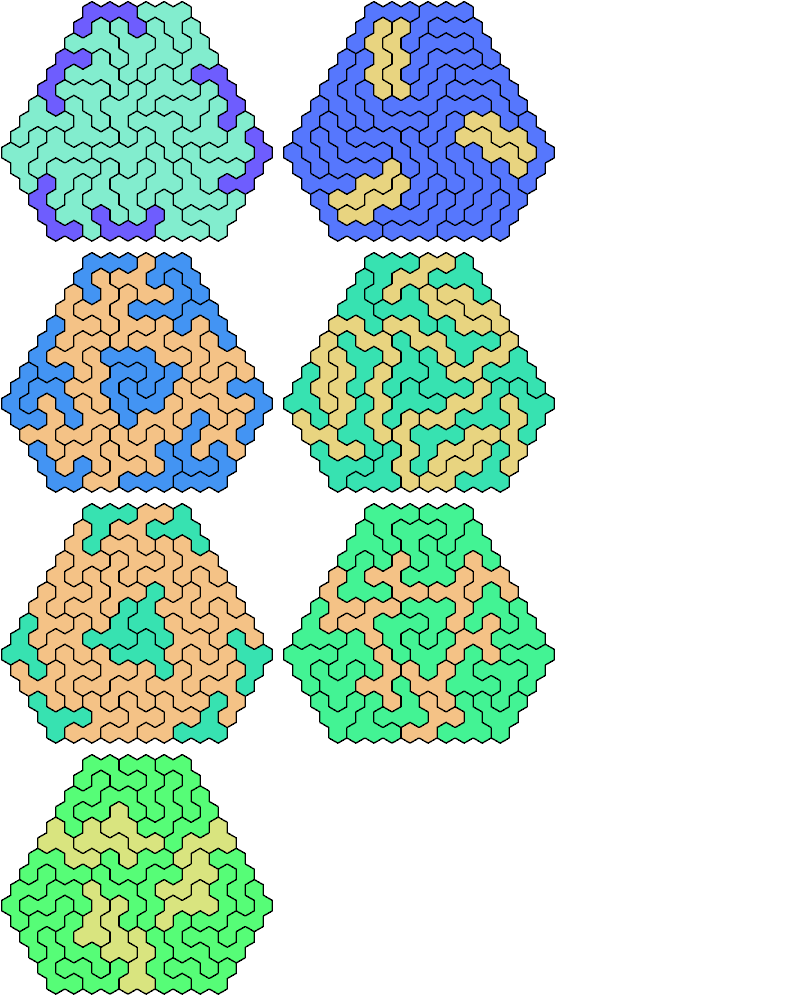
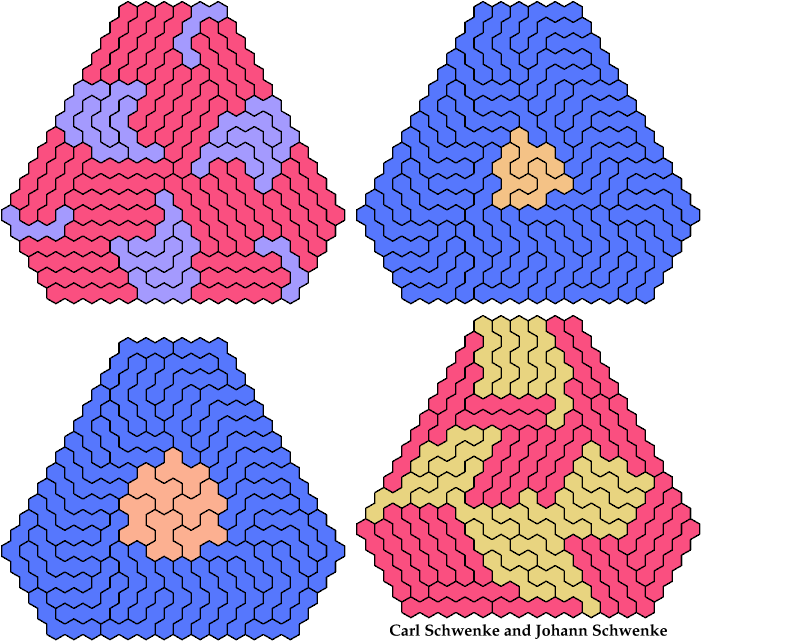
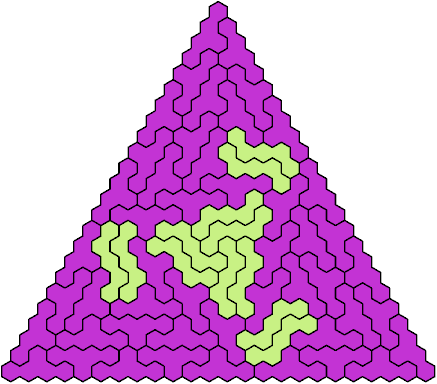
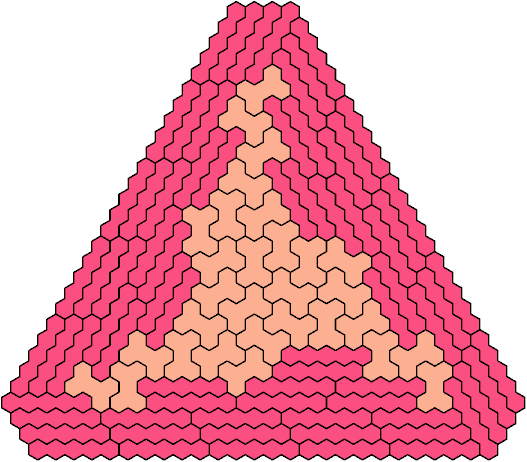
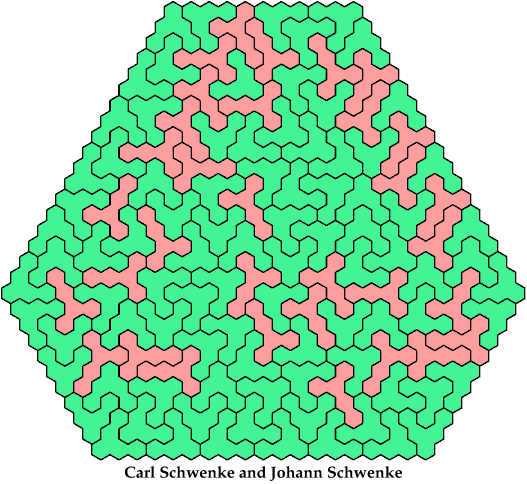
Let a polyhex badge be a polyhex whose cell centers form a convex hexagon whose alternate sides have equal length. Here I study the problem of arranging copies of two given pentahexes to form a badge.
A triangular polyhex is an extreme form of a badge. Many of the solutions below are triangular. See the bottom of the page for non-triangular variants.
Carl Schwenke and Johann Schwenke contributed some improvements.

| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | • | 18 | 9 | 2 | 12 | 33 | 9 | 15 | 9 | 12 | 9 | 9 | 9 | 15 | 126 | 123 | 42 | 12 | 141 | 9 | 9 | 9 |
| C | 18 | • | 5 | 42 | 15 | 12 | 51 | 135 | 18 | 12 | 15 | 12 | 15 | 33 | — | — | — | 18 | 12 | — | 11 | 18 |
| D | 9 | 5 | • | 5 | 9 | 12 | 5 | 12 | 9 | 5 | 5 | 5 | 9 | 5 | 9 | 12 | 12 | 9 | 12 | 9 | 2 | 12 |
| E | 2 | 42 | 5 | • | 12 | 9 | 5 | 9 | 18 | 12 | 9 | 5 | 9 | 9 | 60 | 144 | 12 | 21 | 9 | 9 | 9 | 9 |
| F | 12 | 15 | 9 | 12 | • | 12 | 15 | 27 | 33 | 12 | 12 | 5 | 12 | 18 | — | — | — | 54 | 27 | 15 | 9 | 18 |
| H | 33 | 12 | 12 | 9 | 12 | • | 27 | 33 | — | 12 | 9 | 12 | — | 33 | — | — | 15 | 51 | — | — | 9 | — |
| I | 9 | 51 | 5 | 5 | 15 | 27 | • | 15 | 24 | 9 | 5 | 9 | 18 | 21 | 18 | 2898 | 2124 | 12 | 51 | 102 | 5 | 9 |
| J | 15 | 135 | 12 | 9 | 27 | 33 | 15 | • | 5 | 12 | 9 | 12 | 12 | 12 | — | 66 | — | 12 | — | 18 | 3 | 15 |
| K | 9 | 18 | 9 | 18 | 33 | — | 24 | 5 | • | 12 | 12 | 9 | — | 12 | — | — | 30 | 12 | — | — | 9 | — |
| L | 12 | 12 | 5 | 12 | 12 | 12 | 9 | 12 | 12 | • | 5 | 5 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 9 | 12 |
| N | 9 | 15 | 5 | 9 | 12 | 9 | 5 | 9 | 12 | 5 | • | 9 | 12 | 12 | 15 | 15 | 18 | 12 | 12 | 15 | 9 | 12 |
| P | 9 | 12 | 5 | 5 | 5 | 12 | 9 | 12 | 9 | 5 | 9 | • | 12 | 11 | 12 | 12 | 12 | 12 | 12 | 9 | 9 | 12 |
| Q | 9 | 15 | 9 | 9 | 12 | — | 18 | 12 | — | 12 | 12 | 12 | • | 12 | — | — | 15 | 27 | — | — | 9 | — |
| R | 15 | 33 | 5 | 9 | 18 | 33 | 21 | 12 | 12 | 12 | 12 | 11 | 12 | • | — | — | 15 | 12 | 33 | 141 | 9 | 12 |
| S | 126 | — | 9 | 60 | — | — | 18 | — | — | 12 | 15 | 12 | — | — | • | — | — | 12 | — | — | 9 | — |
| T | 123 | — | 12 | 144 | — | — | 2898 | 66 | — | 12 | 15 | 12 | — | — | — | • | — | 29 | — | — | 15 | — |
| U | 42 | — | 12 | 12 | — | 15 | 2124 | — | 30 | 12 | 18 | 12 | 15 | 15 | — | — | • | 15 | — | — | 9 | 30 |
| V | 12 | 18 | 9 | 21 | 54 | 51 | 12 | 12 | 12 | 12 | 12 | 12 | 27 | 12 | 12 | 29 | 15 | • | 33 | 51 | 9 | 12 |
| W | 141 | 12 | 12 | 9 | 27 | — | 51 | — | — | 12 | 12 | 12 | — | 33 | — | — | — | 33 | • | — | 12 | — |
| X | 9 | — | 9 | 9 | 15 | — | 102 | 18 | — | 12 | 15 | 9 | — | 141 | — | — | — | 51 | — | • | 9 | — |
| Y | 9 | 11 | 2 | 9 | 9 | 9 | 5 | 3 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 15 | 9 | 9 | 12 | 9 | • | 9 |
| Z | 9 | 18 | 12 | 9 | 18 | — | 9 | 15 | — | 12 | 12 | 12 | — | 12 | — | — | 30 | 12 | — | — | 9 | • |


















Last revised 2025-08-15.