Pentahex Pair Frame Tilings

Introduction

A polyhex frame is a regular hexagonal polyhex with a centered regular hexagonal hole. Erich Friedman studied polyomino frame tilings in his Math Magic problem for January 2008. At my suggestion, he added frame tilings for polyiamonds and polyhexes.

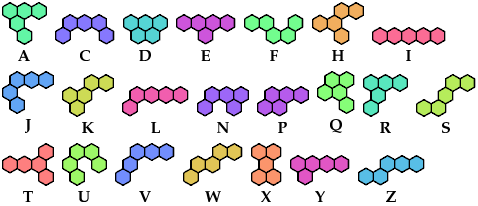
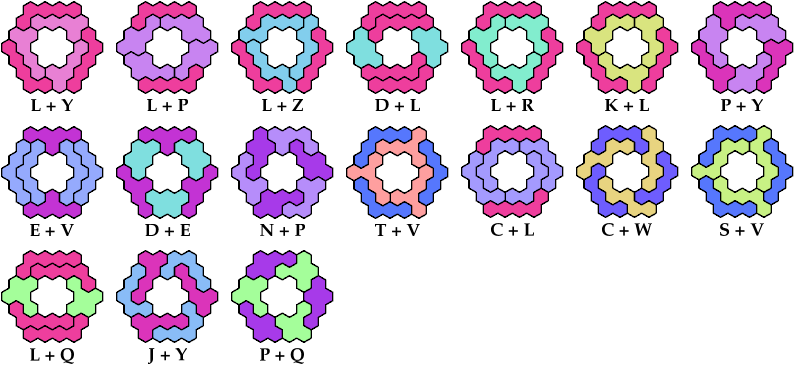
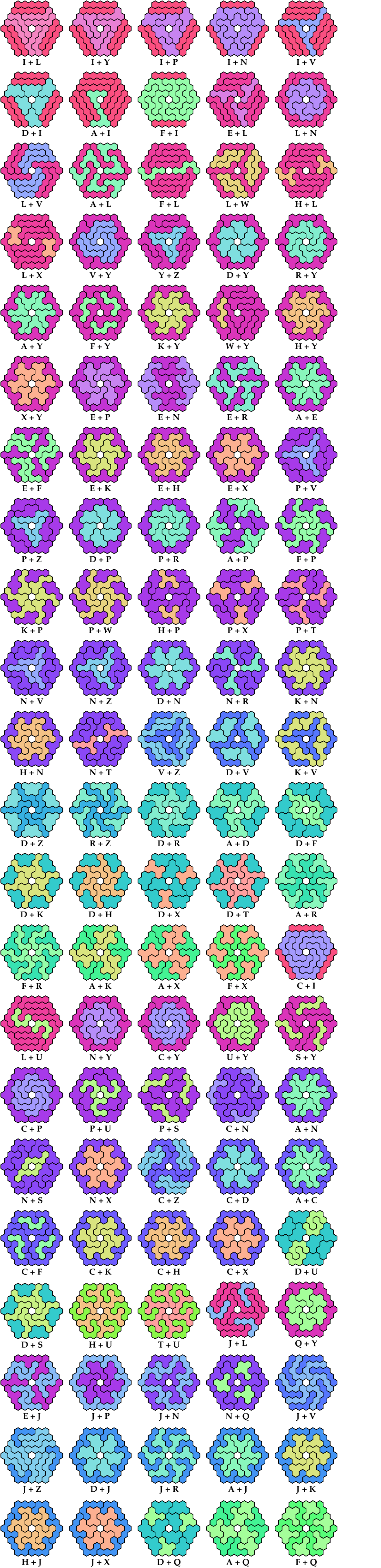
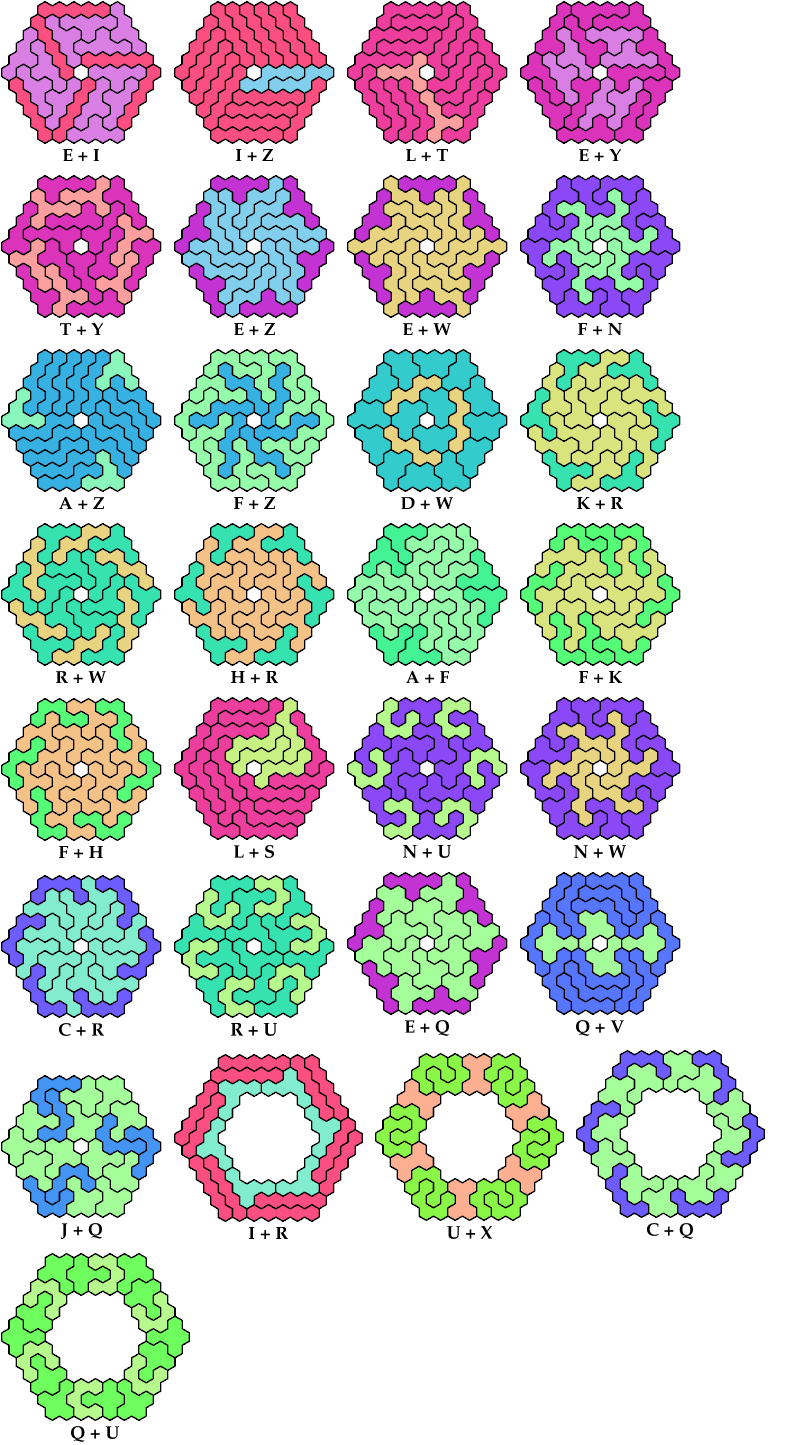
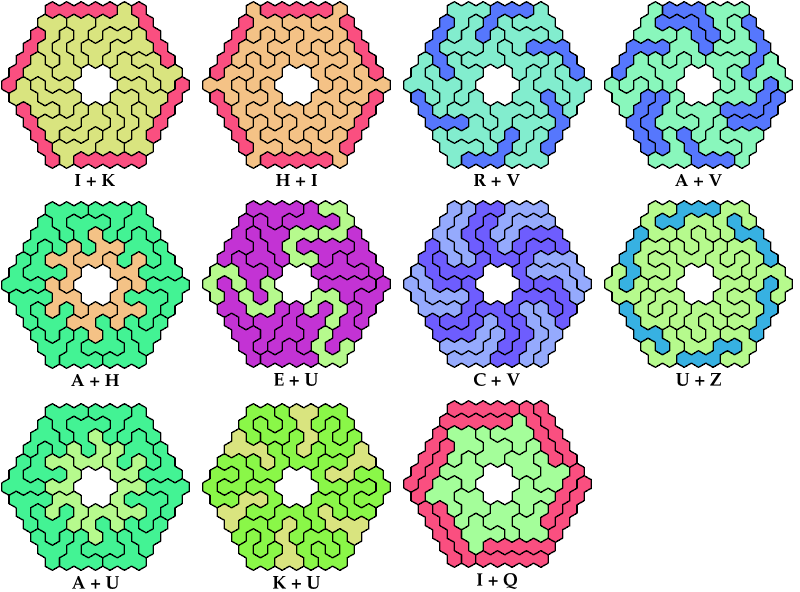
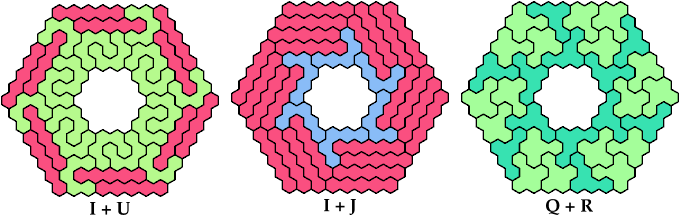
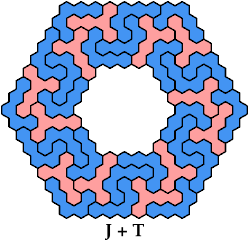
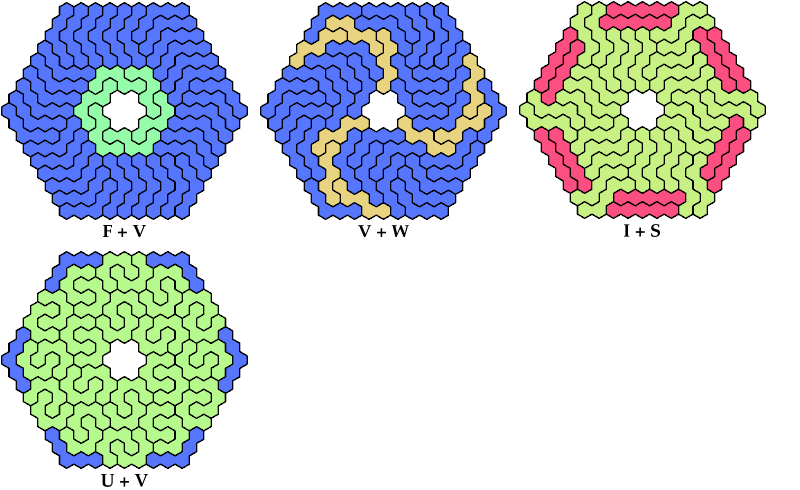
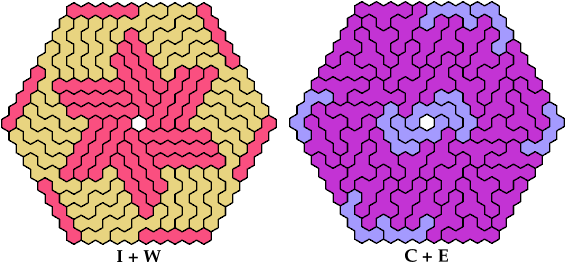
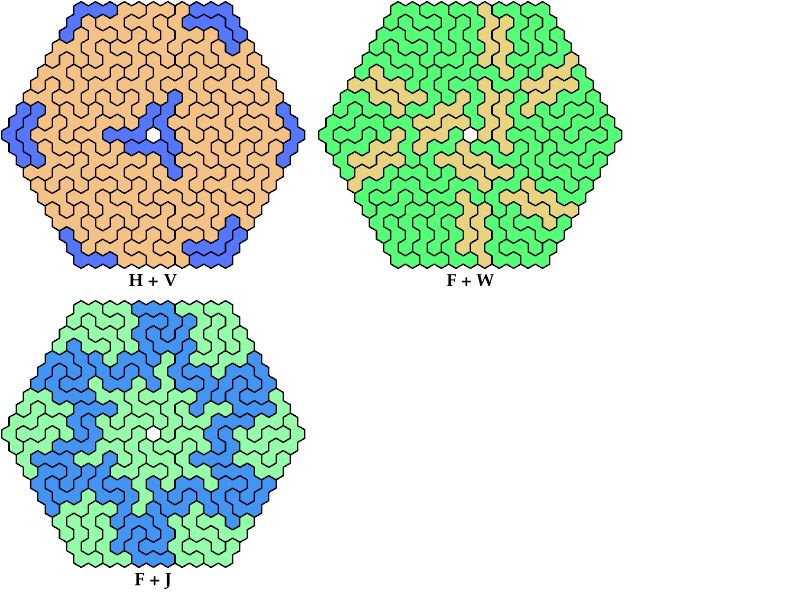
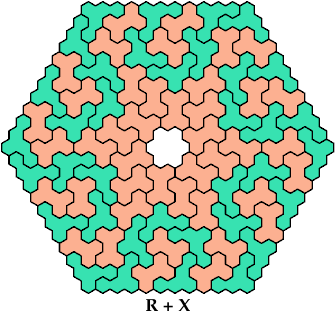
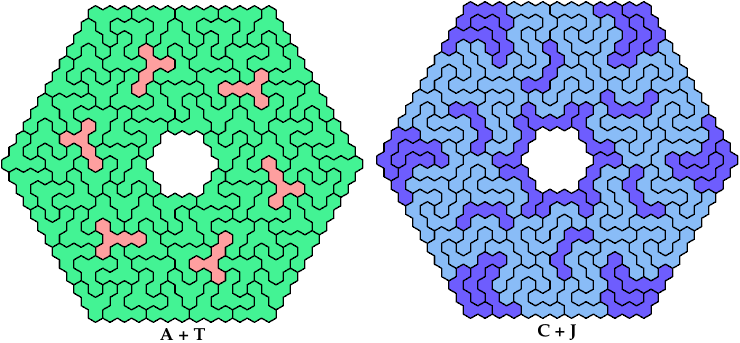
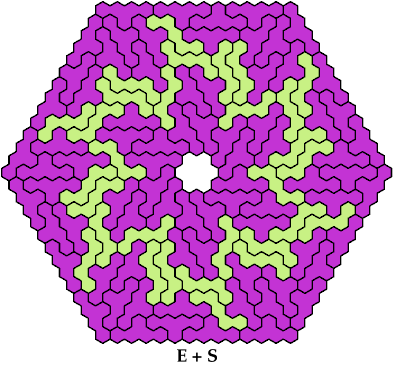
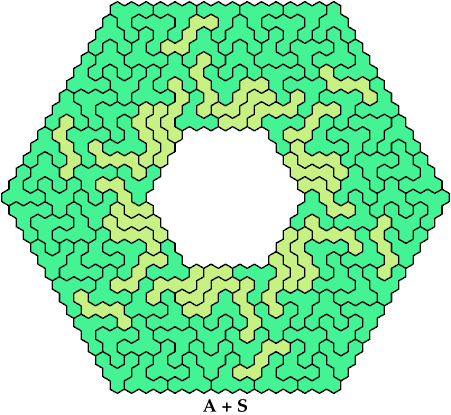
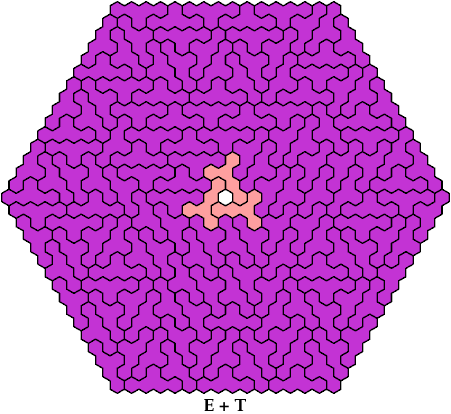
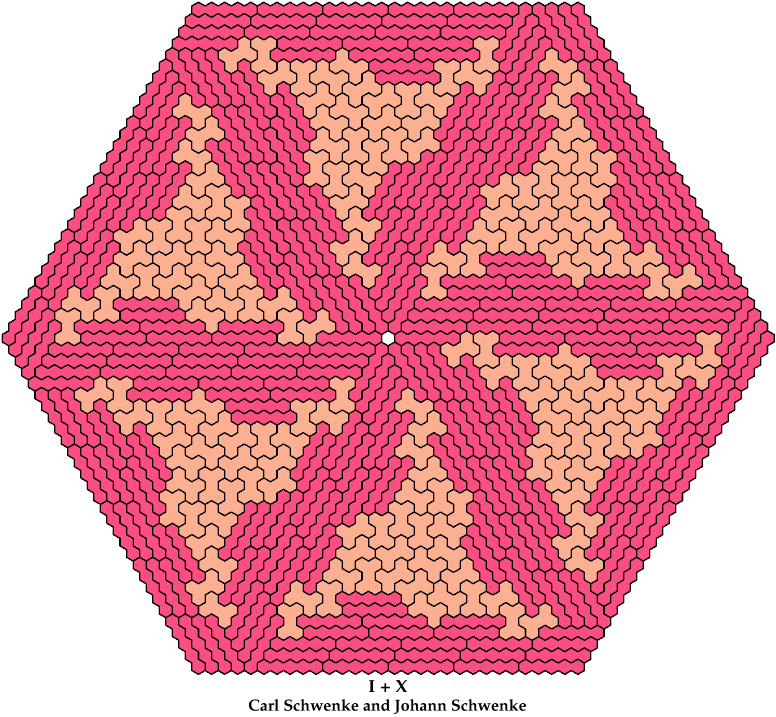
On this page, for each pair of pentahexes, I show a frame tiling with the fewest known cells, using at least one copy of each pentahex of the pair. If you find a smaller solution or solve an unsolved case, please write.

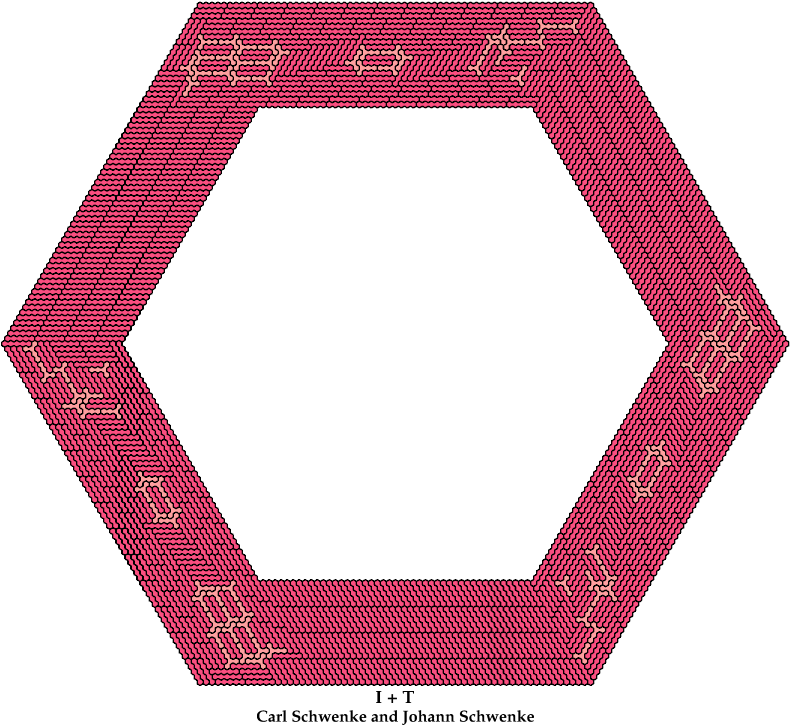
Carl Schwenke and Johann Schwenke solved the pairs 5I+5X and 5I+5T.

Catalogue of Pentahexes

Table of Results

	A	C	D	E	F	H	I	J	K	L	N	P	Q	R	S	T	U	V	W	X	Y	Z
A	•	12	12	12	18	24	12	12	12	12	12	12	12	12	126	90	24	24	114	12	12	18
C	12	•	12	54	12	12	12	90	12	6	12	12	18	18	—	—	—	24	6	12	12	12
D	12	12	•	6	12	12	12	12	12	6	12	12	12	12	12	12	12	12	18	12	12	12
E	12	54	6	•	12	12	18	12	12	12	12	12	18	12	108	144	24	6	18	12	18	18
F	18	12	12	12	•	18	12	66	18	12	18	12	12	12	—	—	—	42	66	12	12	18
H	24	12	12	12	18	•	24	12	—	12	12	12	—	18	—	—	12	66	—	—	12	—
I	12	12	12	18	12	24	•	30	24	12	12	12	24	18	42	1332	30	12	54	522	12	18
J	12	90	12	12	66	12	30	•	12	12	12	12	18	12	—	36	—	12	—	12	6	12
K	12	12	12	12	18	—	24	12	•	6	12	12	—	18	—	—	24	12	—	—	12	—
L	12	6	6	12	12	12	12	12	6	•	12	6	6	6	18	18	12	12	12	12	6	6
N	12	12	12	12	18	12	12	12	12	12	•	6	12	12	12	12	18	12	18	12	12	12
P	12	12	12	12	12	12	12	12	12	6	6	•	6	12	12	12	12	12	12	12	6	12
Q	12	18	12	18	12	—	24	18	—	6	12	6	•	30	—	—	18	18	—	—	12	—
R	12	18	12	12	12	18	18	12	18	6	12	12	30	•	—	—	18	24	18	78	12	12
S	126	—	12	108	—	—	42	—	—	18	12	12	—	—	•	—	—	6	—	—	12	—
T	90	—	12	144	—	—	1332	36	—	18	12	12	—	—	—	•	12	6	—	—	18	—
U	24	—	12	24	—	12	30	—	24	12	18	12	18	18	—	12	•	42	—	18	12	24
V	24	24	12	6	42	66	12	12	12	12	12	12	18	24	6	6	42	•	42	72	12	12
W	114	6	18	18	66	—	54	—	—	12	18	12	—	18	—	—	—	42	•	—	12	—
X	12	12	12	12	12	—	522	12	—	12	12	12	—	78	—	—	18	72	—	•	12	—
Y	12	12	12	18	12	12	12	6	12	6	12	6	12	12	12	18	12	12	12	12	•	12
Z	18	12	12	18	18	—	18	12	—	6	12	12	—	12	—	—	24	12	—	—	12	•