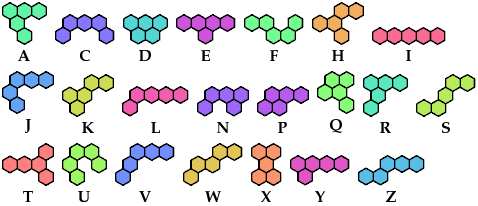
Carl Schwenke and Johann Schwenke contributed solutions.

| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | • | 6 | 4 | 4 | 6 | — | 6 | 6 | 4 | 4 | 6 | 3 | 4 | 6 | — | — | 8 | — | — | 3 | 6 | 6 |
| C | 6 | • | 6 | 42 | — | — | 44 | — | — | 18 | 6 | 6 | — | — | — | — | — | — | — | — | 9 | — |
| D | 4 | 6 | • | 6 | 12 | 12 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 12 | 6 | 3 | 12 | 3 | 3 | 12 |
| E | 4 | 42 | 6 | • | 4 | 6 | 6 | 4 | 6 | 8 | 6 | 4 | 6 | 4 | 27 | 132 | 8 | 16 | 6 | 5 | 6 | 8 |
| F | 6 | — | 12 | 4 | • | — | 44 | — | — | 22 | 12 | 8 | — | — | — | — | — | — | — | — | 4 | — |
| H | — | — | 12 | 6 | — | • | 28 | — | — | 14 | 8 | 8 | — | — | — | — | — | — | — | — | 10 | — |
| I | 6 | 44 | 3 | 6 | 44 | 28 | • | 21 | 14 | 3 | 4 | 3 | 22 | 16 | 33 | 238 | 174 | 6 | 33 | 156 | 3 | 12 |
| J | 6 | — | 4 | 4 | — | — | 21 | • | 16 | 18 | 4 | 12 | — | 4 | — | — | — | — | — | — | 4 | — |
| K | 4 | — | 4 | 6 | — | — | 14 | 16 | • | 4 | 6 | 6 | — | — | — | — | — | 4 | — | — | 6 | — |
| L | 4 | 18 | 4 | 8 | 22 | 14 | 3 | 18 | 4 | • | 4 | 3 | 14 | 7 | 18 | 14 | 16 | 6 | 4 | 21 | 4 | 4 |
| N | 6 | 6 | 4 | 6 | 12 | 8 | 4 | 4 | 6 | 4 | • | 4 | 6 | 10 | 16 | 6 | 18 | 12 | 16 | 3 | 4 | 4 |
| P | 3 | 6 | 4 | 4 | 8 | 8 | 3 | 12 | 6 | 3 | 4 | • | 6 | 6 | 3 | 12 | 6 | 6 | 6 | 7 | 4 | 4 |
| Q | 4 | — | 4 | 6 | — | — | 22 | — | — | 14 | 6 | 6 | • | — | — | — | — | — | — | — | 4 | — |
| R | 6 | — | 3 | 4 | — | — | 16 | 4 | — | 7 | 10 | 6 | — | • | — | — | — | — | — | — | 3 | — |
| S | — | — | 3 | 27 | — | — | 33 | — | — | 18 | 16 | 3 | — | — | • | — | — | 3 | — | — | 3 | — |
| T | — | — | 12 | 132 | — | — | 238 | — | — | 14 | 6 | 12 | — | — | — | • | — | — | — | — | 10 | — |
| U | 8 | — | 6 | 8 | — | — | 174 | — | — | 16 | 18 | 6 | — | — | — | — | • | — | — | — | 4 | — |
| V | — | — | 3 | 16 | — | — | 6 | — | 4 | 6 | 12 | 6 | — | — | 3 | — | — | • | — | — | 4 | 4 |
| W | — | — | 12 | 6 | — | — | 33 | — | — | 4 | 16 | 6 | — | — | — | — | — | — | • | — | 6 | — |
| X | 3 | — | 3 | 5 | — | — | 156 | — | — | 21 | 3 | 7 | — | — | — | — | — | — | — | • | 5 | — |
| Y | 6 | 9 | 3 | 6 | 4 | 10 | 3 | 4 | 6 | 4 | 4 | 4 | 4 | 3 | 3 | 10 | 4 | 4 | 6 | 5 | • | 4 |
| Z | 6 | — | 12 | 8 | — | — | 12 | — | — | 4 | 4 | 4 | — | — | — | — | — | 4 | — | — | 4 | • |


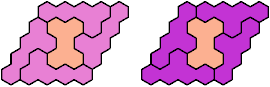

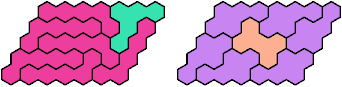

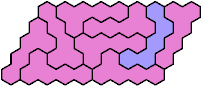










Last revised 2025-09-10.