In March 2003, Erich Friedman's Math Magic studied the problem of arranging copies of a single polyhex to form a triangular polyhex.
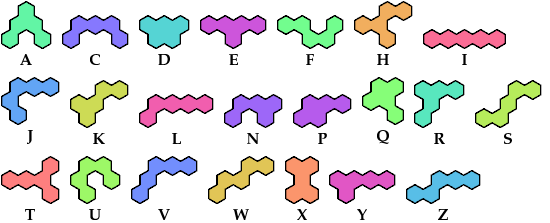
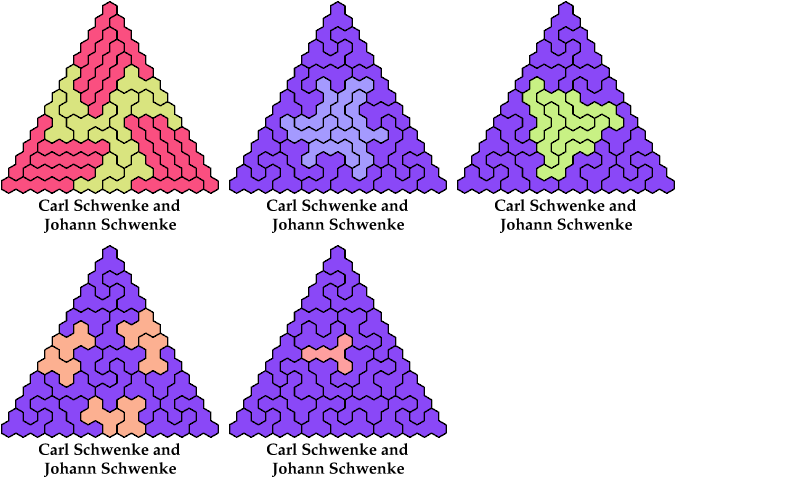
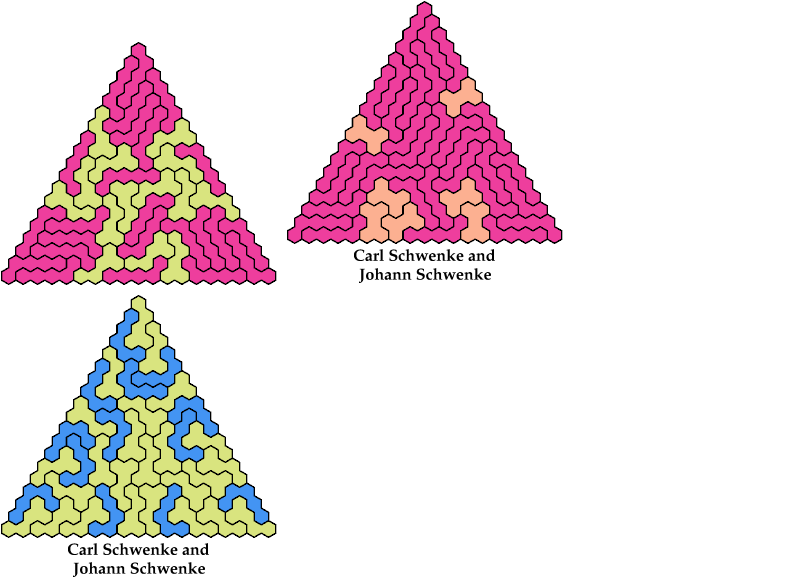
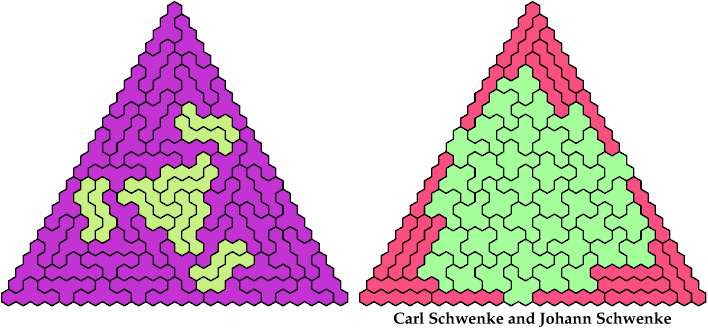
Here I study the related problem of arranging copies of two pentahexes to form a triangular polyhex. All the triangular polyhexes shown are the smallest known. Thanks to Johann Schwenke and Carl Schwenke for suggesting this problem.

| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 20 | 9 | 4 | 14 | ? | 9 | 20 | 9 | 14 | 9 | 9 | 9 | 14 | ? | ? | 20 | ? | ? | 9 | 9 | 9 | |
| C | 20 | 9 | 20 | ? | ? | ? | ? | ? | ? | 15 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 10 | ? | |
| D | 9 | 9 | 9 | 9 | 14 | 9 | 14 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 14 | 14 | 9 | 14 | 9 | 4 | 14 | |
| E | 4 | 20 | 9 | 14 | 9 | 10 | 9 | 14 | 14 | 9 | 9 | 9 | 9 | 24 | 54 | 14 | 14 | 9 | 9 | 9 | 9 | |
| F | 14 | ? | 9 | 14 | ? | 30 | ? | ? | ? | 14 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| H | ? | ? | 14 | 9 | ? | 20 | ? | ? | ? | 9 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| I | 9 | ? | 9 | 10 | 30 | 20 | 20 | 15 | 9 | 9 | 9 | 24 | 14 | 29 | ? | ? | 30 | 30 | ? | 9 | 9 | |
| J | 20 | ? | 14 | 9 | ? | ? | 20 | 19 | ? | 9 | ? | ? | 14 | ? | ? | ? | ? | ? | ? | 5 | ? | |
| K | 9 | ? | 9 | 14 | ? | ? | 15 | 19 | 19 | 14 | 9 | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| L | 14 | ? | 9 | 14 | ? | ? | 9 | ? | 19 | 9 | ? | ? | 14 | ? | ? | ? | ? | ? | 19 | 9 | ? | |
| N | 9 | 15 | 9 | 9 | 14 | 9 | 9 | 9 | 14 | 9 | 9 | 14 | 14 | 15 | 15 | 20 | 14 | 14 | 15 | 9 | 14 | |
| P | 9 | ? | 9 | 9 | ? | ? | 9 | ? | 9 | ? | 9 | ? | 10 | ? | ? | ? | ? | ? | 9 | 9 | ? | |
| Q | 9 | ? | 9 | 9 | ? | ? | 24 | ? | ? | ? | 14 | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| R | 14 | ? | 9 | 9 | ? | ? | 14 | 14 | ? | 14 | 14 | 10 | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| S | ? | ? | 9 | 24 | ? | ? | 29 | ? | ? | ? | 15 | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| T | ? | ? | 14 | 54 | ? | ? | ? | ? | ? | ? | 15 | ? | ? | ? | ? | ? | ? | ? | ? | 14 | ? | |
| U | 20 | ? | 14 | 14 | ? | ? | ? | ? | ? | ? | 20 | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| V | ? | ? | 9 | 14 | ? | ? | 30 | ? | ? | ? | 14 | ? | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| W | ? | ? | 14 | 9 | ? | ? | 30 | ? | ? | ? | 14 | ? | ? | ? | ? | ? | ? | ? | ? | 14 | ? | |
| X | 9 | ? | 9 | 9 | ? | ? | ? | ? | ? | 19 | 15 | 9 | ? | ? | ? | ? | ? | ? | ? | 9 | ? | |
| Y | 9 | 10 | 4 | 9 | 9 | 9 | 9 | 5 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 14 | 9 | 9 | 14 | 9 | 9 | |
| Z | 9 | ? | 14 | 9 | ? | ? | 9 | ? | ? | ? | 14 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 9 |





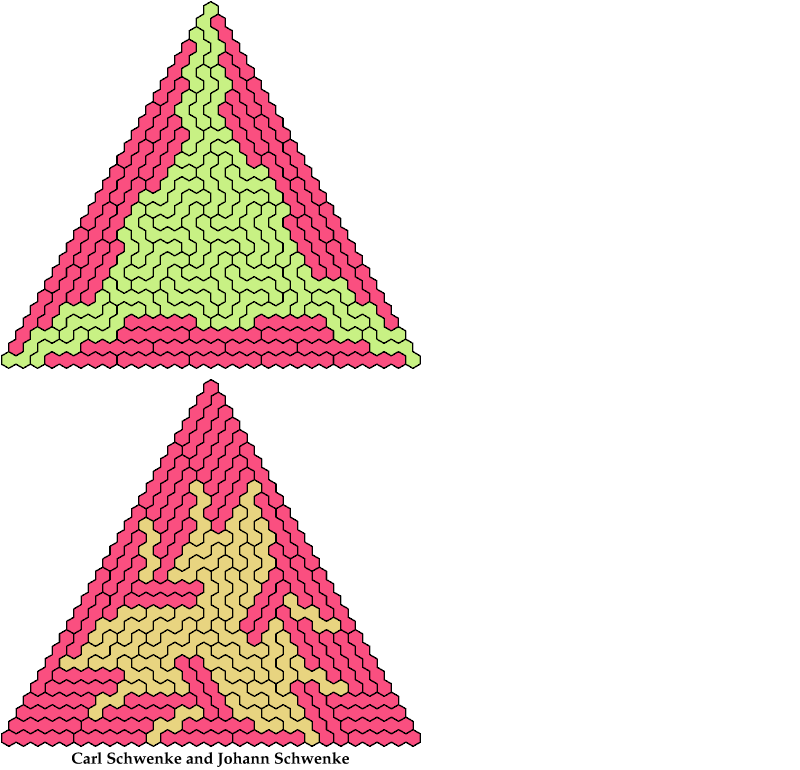
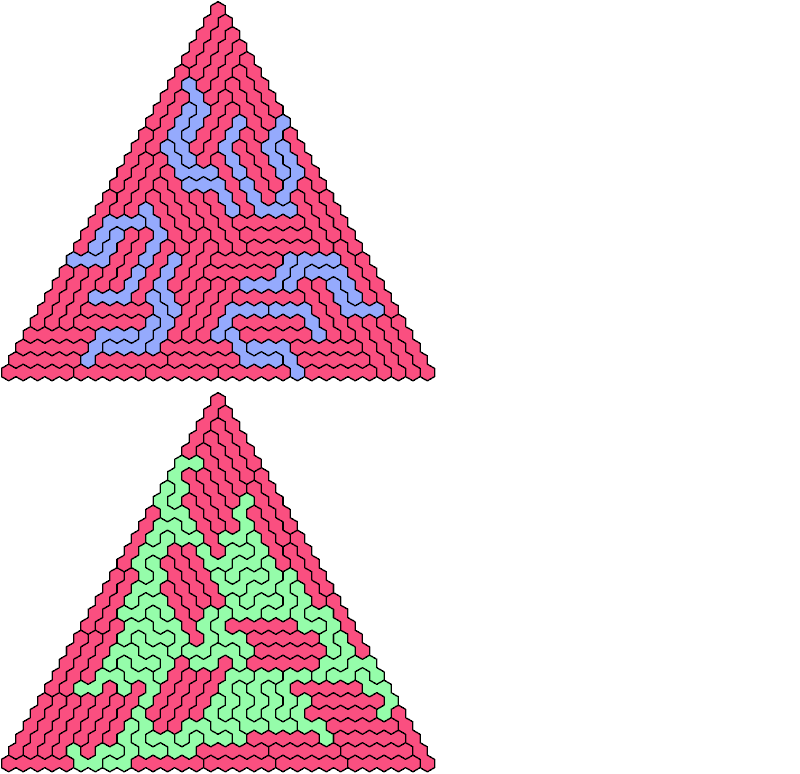

Last revised 2025-09-04.