Tiling a Triangle Polyhex with a Polyhex
Introduction
A polyhex
is a plane figure formed by joining equal regular hexagons
edge to edge.
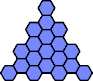
There are two kinds of equilateral triangular polyhexes:
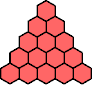
| 
|
| Straight
| Ragged
|
Here I show the smallest triangular polyhex of each type
that various small polyhexes can tile,
and identify what larger triangles they can tile.
Polyhexes not shown cannot tile a triangular polyhex, so far as is known.
If you find a smaller solution, or a solution for another
polyhex, please write.
Most of these results for straight triangles
are taken from Erich Friedman's Math Magic
for 2003-03.
There Erich presents results by Berend Jan van der Zwaag, Brendan Owen,
Claudio Baiocchi, Jeremy Galvagni,
Andrew Clarke, and Mike Reid.
See also Tiling a Hexagon
Polyhex with a Heptahex.
Carl Schwenke and Johann Schwenke identified missing information
and provided new solutions.
Monohex
| Tile | Smallest Triangle | Sizes |
|---|
 |  | all |
Dihex
| Tile | Smallest Triangle | Sizes |
|---|
 | 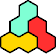 | n ≡ 0 or 3 (mod 4) |
Trihexes
| Tile | Smallest Triangle | Sizes |
|---|
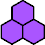 |  | n ≡ 0, 2, 9, or 11 (mod 12) |
Tetrahexes
| Tile | Smallest Triangle | Sizes |
|---|
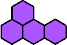 |  | n
≡ 0 or 7 (mod 8) |
Pentahexes
| Tile | Smallest Triangle | Sizes |
|---|
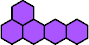 |  | n
≡ 0 or 4 (mod 5), except 4 and 10 |
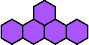 |  | n
= 5, …, 54, …, 59, 60, 60k−1,
…, 65, …,
119, 120, …, ?
(Carl Schwenke and Johann Schwenke) |
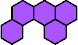 |  | n
≡ 0 or 4 (mod 5), except 4, 9, 10, 14, and 19 (Andrew Clarke)
|
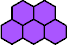 |  | n
≡ 0 or 4 (mod 5), except 4 and 10 |
Hexahexes
| Tile | Smallest Triangle | Sizes |
|---|
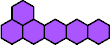 |  | n
≡ 0, 3, 20, or 23 (mod 24), except 3 |
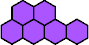 |  | n
≡ 0, 3, 8, or 11 (mod 12), except 3, 8, 11, and 12 |
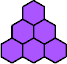 |  | n
= 3 … ? |
Heptahexes
| Tile | Smallest Triangle | Sizes |
|---|
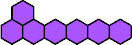
|  | n
= 27, 28, 28k−1, 28k, 35, 41, 42, … ? |
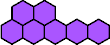 |  | n
≡ 0 or 6 (mod 7), except 7, 13, 14, 20 |
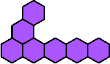 |  | n
= 6, … ? |
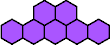 |  | n
= 6, … ? |
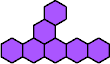 |  | n
= 6, … ? |
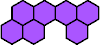 |  | n
= 6, … ? |
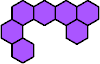 |  | n
= 6, … ? |
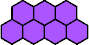 |  | n
≡ 0 or 6 (mod 7), except 7, 13, 14, 20 |
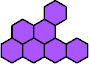 |  | n
= 6, … ? |
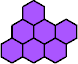 |  | n
= 6, 27, 35, 41, 42, 48, 56, 62, 63, 69, … ? |
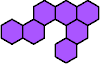 |  | n
= 6, … ? |
Monohex
| Tile | Smallest Triangle | Sizes |
|---|
 |  | all |
Dihex
| Tile | Smallest Triangle | Sizes |
|---|
 | 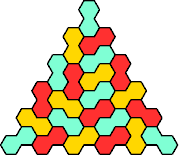 | n
≡ 2 or 3 (mod 4), except 2 and 3
|
Tetrahexes
| Tile | Smallest Triangle | Sizes |
|---|
 |  | n
≡ 2 or 7 (mod 8), except 2 and 7
|
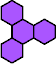 |  | n
= 2
|
Pentahexes
| Tile | Smallest Triangle | Sizes |
|---|
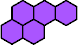 |  | n
≡ 3 (mod 5), except 3 and 8
|
| Tile | Smallest Triangle | Sizes |
|---|
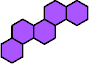 |  | n
= 18, 23, 28, 33, … ?
|
Last revised 2025-09-08.
Back to Polyhex Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]



























































