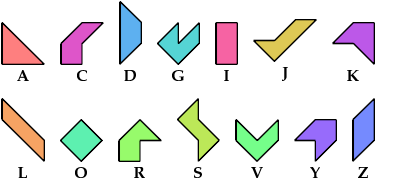
Tiling a Polyabolo at Scale 2 with Two Tetraboloes
A tetrabolo is a figure made of four isosceles
right triangles joined
edge to edge.
There are 14 such figures, not distinguishing reflections and rotations.
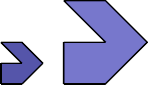
Here I study the problem of arranging copies of two tetraboloes
to form some polyabolo that has been scaled up by a factor of 2.
See also
This table shows the smallest total number of copies
of two tetraboloes known to be
able to tile some polyabolo enlarged by a scale factor of 2,
using at least one copy of each tetrabolo.
The blue indexes are links to tilings by the specified tetrabolo alone.
| A | C | D | G | I | J | K | L | O | R | S | V | Y | Z |
|---|
| A | *
| 10
| 5
| 5
| 3
| 5
| 20
| 3
| 5
| 5
| ?
| 12
| 16
| 3
|
|---|
| C | 10
| *
| 8
| 16
| 6
| 8
| 8
| 6
| ?
| 8
| 20
| 24
| 6
| 6
|
|---|
| D | 5
| 8
| *
| 6
| 6
| 2
| 4
| 6
| 8
| 8
| 6
| 8
| 7
| 4
|
|---|
| G | 5
| 16
| 6
| *
| ?
| 4
| 6
| 6
| 4
| 8
| 10
| 8
| 5
| 6
|
|---|
| I | 3
| 6
| 6
| ?
| *
| 6
| 6
| 4
| ?
| 6
| ?
| ?
| 6
| 4
|
|---|
| J | 5
| 8
| 2
| 4
| 6
| *
| 4
| 6
| 4
| 4
| 10
| 8
| 3
| 6
|
|---|
| K | 20
| 8
| 4
| 6
| 6
| 4
| *
| 6
| 28
| 8
| ?
| 12
| 12
| 4
|
|---|
| L | 3
| 6
| 6
| 6
| 4
| 6
| 6
| *
| 6
| 6
| ?
| ?
| 4
| 4
|
|---|
| O | 5
| ?
| 8
| 4
| ?
| 4
| 28
| 6
| *
| 8
| ?
| 8
| ?
| 6
|
|---|
| R | 5
| 8
| 8
| 8
| 6
| 4
| 8
| 6
| 8
| *
| 20
| 6
| 8
| 6
|
|---|
| S | ?
| 20
| 6
| 10
| ?
| 10
| ?
| ?
| ?
| 20
| *
| ?
| ?
| ?
|
|---|
| V | 12
| 24
| 8
| 8
| ?
| 8
| 12
| ?
| 8
| 6
| ?
| *
| ?
| 4
|
|---|
| Y | 16
| 6
| 7
| 5
| 6
| 3
| 12
| 4
| ?
| 8
| ?
| ?
| *
| ?
|
|---|
| Z | 3
| 6
| 4
| 6
| 4
| 6
| 4
| 4
| 6
| 6
| ?
| 4
| ?
| *
|
|---|
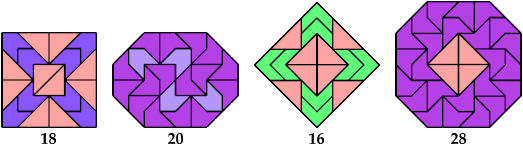
So far as I know, these solutions
use as few tiles as possible. They are not necessarily uniquely minimal.
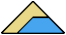
2 Tiles
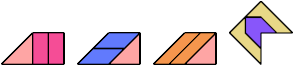
3 Tiles
4 Tiles

5 Tiles

6 Tiles
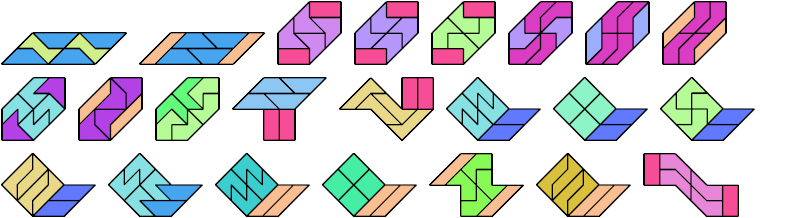
7 Tiles
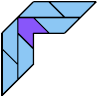
8 Tiles
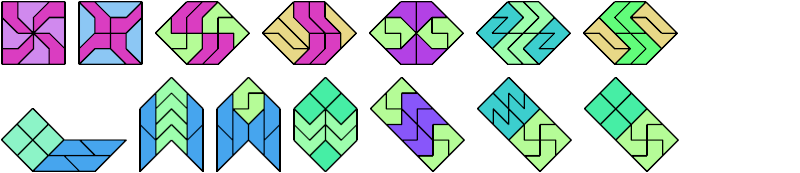
10 Tiles
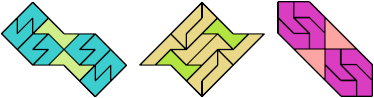
12 Tiles
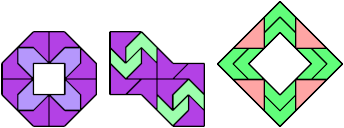
16 Tiles
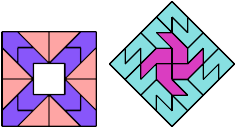
20 Tiles
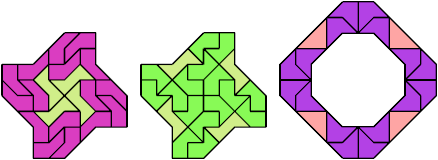
24 Tiles

28 Tiles
Last revised 2025-05-05.
Back to Polyabolo and Polyfett Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]
















