

 | Similar Polyaboloes Tiling a Square. Join variously sized copies of a polyabolo to make a square. |
 | Similar Polyaboloes Tiling a Rectangle. Join variously sized copies of a polyabolo to make a rectangle. |
 | Tiling a Rectangle with Two Scaled Pentaboloes. Arrange scalable copies of two pentaboloes to form a rectangle. |
 | Tiling a Rectangle with a Scaled Tetrabolo and a Scaled Pentabolo. Arrange scalable copies of a tetrabolo and a pentabolo to form a rectangle. |
 | Rectification Numbers for Polyaboloes. Pack copies of a polyabolo into some rectangle, leaving as few cells vacant as possible. |
 | Oblique Rectification Numbers for Polyaboloes. Pack copies of a polyabolo into some oblique rectangle, leaving as few cells vacant as possible. |
 | Similar Polyfetts Tiling a Square. Tile a square with variously sized copies of a polyfett. |
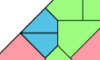 | Polyabolo Irreptiles. Join variously sized copies of a polyabolo to make a replica of itself. |
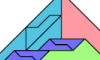 | Similar Polyaboloes Tiling a Triangle. Join variously sized copies of a polyabolo to make a triangle. |
 | Similar Polyaboloes Tiling a Right Trapezial Triabolo. Join variously sized copies of a polyabolo to make a right trapezoidal triabolo. |
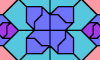 | Similar Polyaboloes Tiling an Octagon. Join variously sized copies of a polyabolo to make an octagon. |
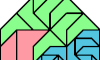 | Similar Polyaboloes Tiling a Home Plate Hexabolo. Join variously sized copies of a polyabolo to make a home plate. |
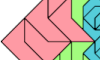 | Similar Polyaboloes Tiling a Crown Heptabolo. Join variously sized copies of a polyabolo to make a crown heptabolo. |
 | Tiling a Chamfered Rectangle with a Polyabolo. Arrange copies of a polyabolo to form a rectangle with its corners clipped. |
 | Tiling a Chamfered Rectangle with Two Tetraboloes. Arrange copies of two tetraboloes to form a rectangle with its corners clipped. |
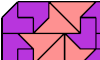 | Tiling a Chamfered Rectangle with Two Pentaboloes. Arrange copies of two pentaboloes to form a rectangle with its corners clipped. |
 | Tiling a Chamfered Rectangle with Three Pentaboloes. Arrange copies of three pentaboloes to form a rectangle with its corners clipped. |
 | Similar Polyaboloes Forming a Convex Shape. Join variously sized copies of a polyabolo to make a convex shape. |
 | Convex Polygons from Pairs of Polytans. With copies of two given polytans make the smallest convex polytan. |
 | Tiling a Polyabolo at Scale 2 with Pairs of Tetraboloes. With copies of two given tetraboloes make the smallest polyabolo that has been scaled up by a factor of 2. |
 | Polytan Bireptiles. Join two copies of a polytan, then dissect the result into equal smaller copies of it. |
 | Scaled Polytan Tetrads. Join four similar polytans so that each borders the other three. |
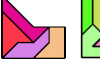 | Similar Pentatan Figures 2–2√2–3√2. Arrange the 30 pentatans to make three copies of the same pentatan at scales 2, 2√2, and 3√2. |
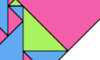 | Tiling a Polytan With Unequal Monotans. Dissect an arbitrary polytan into isosceles right triangles, all of different sizes. |
 | Strong Surround Numbers for Polyaboloes. Surround a polyabolo, including its corners, with as few copies of itself as possible. |
 | Polyfett Irreptiles. Tile a polyfett with smaller copies of itself, not necessarily equal. |
 | Similar Polyfetts Tiling a Triangle. Tile a triangle with variously sized copies of a polyfett. |
 | Tiling Right Trapezia with Scaled Pentabolo Pairs. Use scaled copies of two pentaboloes to form a right trapezium (trapezoid in Canada and U.S.). |
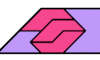 | Tiling Isosceles Trapezia with Scaled Pentabolo Pairs. Use scaled copies of two pentaboloes to form an isosceles trapezium (trapezoid in Canada and U.S.). |