Tiling Right Trapezia with Scaled Pentabolo Pairs

Introduction

A pentabolo or pentatan is a plane figure formed by joining five equal isosceles right triangles edge to equal edge. There are 30 different pentaboloes, not counting reflections and rotations.

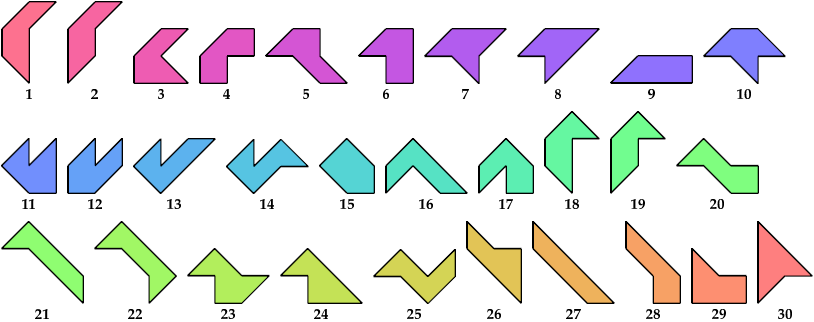
A scaled pentabolo is a pentabolo whose size may be altered without changing its shape. In geometric terms, it is a family of similar pentaboloes.

A trapezium (trapezoid in Canada and the U.S.) is a plane figure with four sides, two of them parallel. A right trapezium is a trapezium with one side perpendicular to the parallel sides.

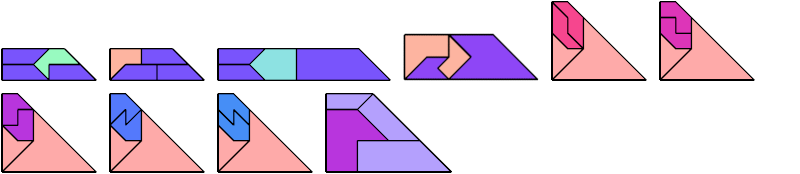
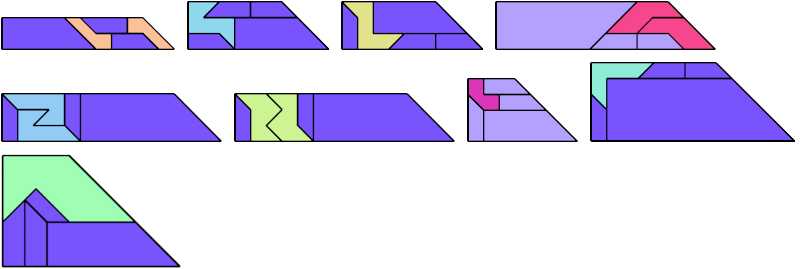
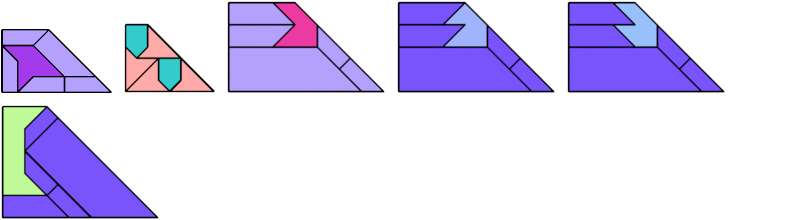
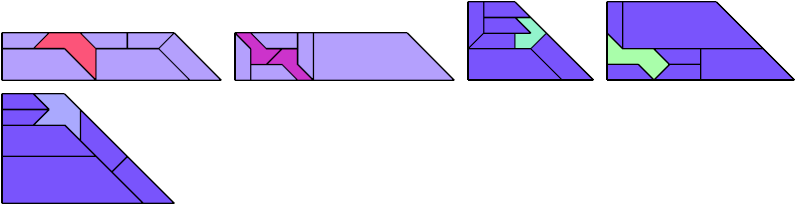
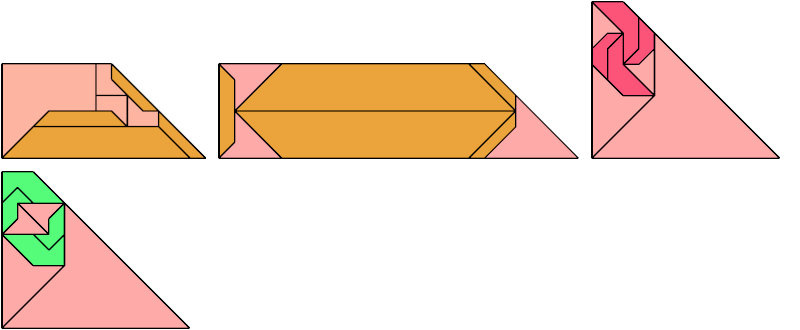
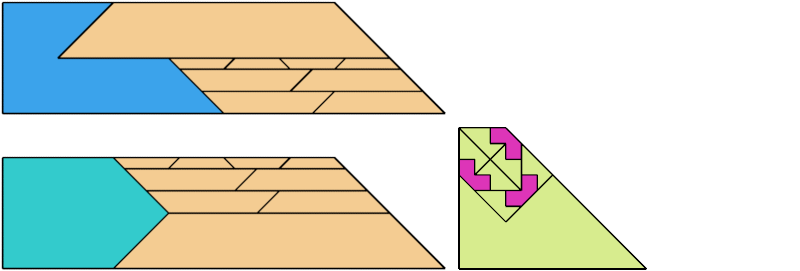
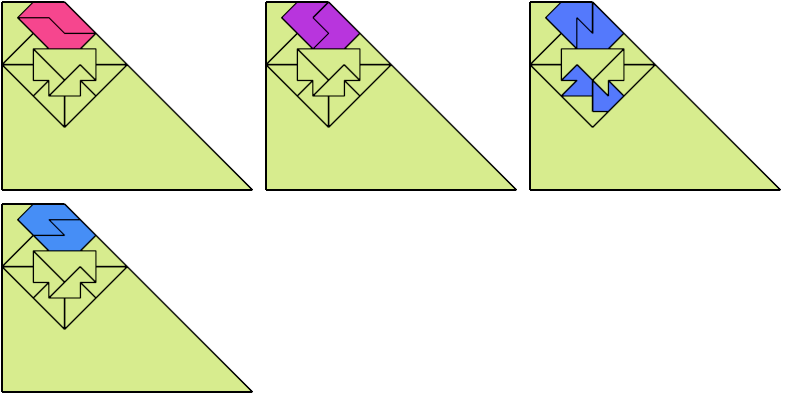
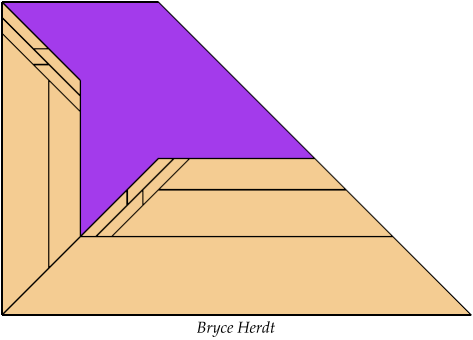
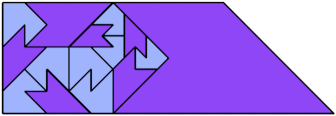
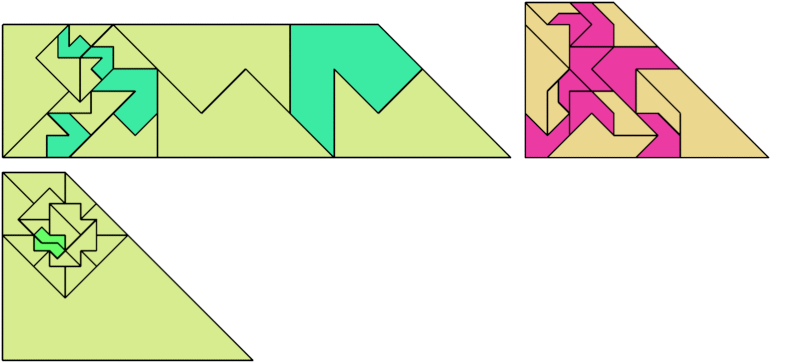
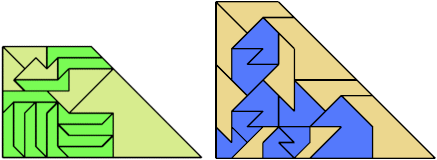
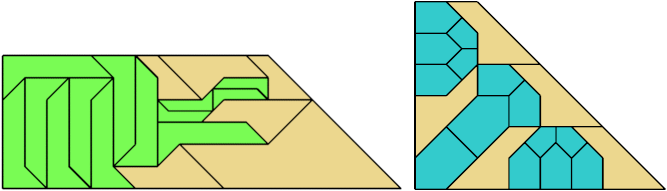
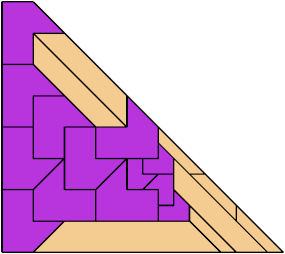
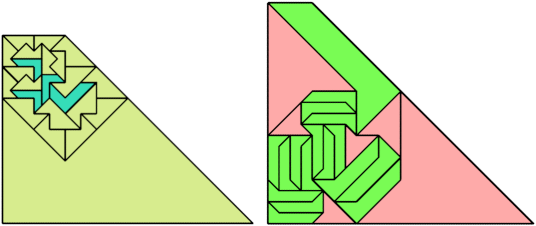
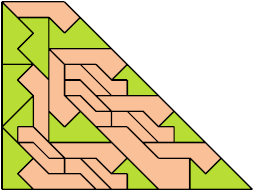
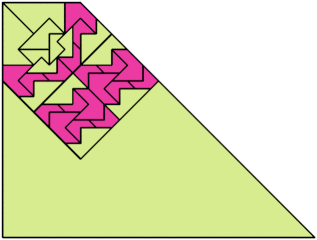
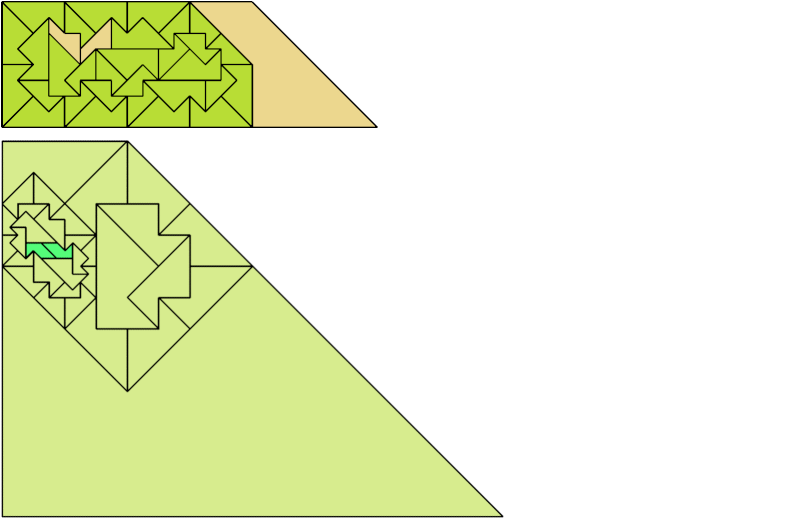
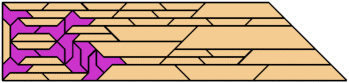
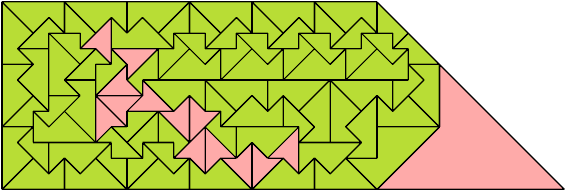
For every pair of scaled pentaboloes, I show a trapezium that they can tile, using at least one of each, and using as few tiles as known to be possible. If you find a smaller solution or solve an unsolved case, please write.

Bryce Herdt found new and improved solutions.

See also

Table of Results

Each figure indicates the number of tiles in the tiling. Pairs not shown cannot tile a right trapezium.

Theoretically, scaled pentabolo 24 and any other scaled pentabolo can together tile a trapezium. I do not have tilings for all such pairs of scaled pentaboloes.

 123456789101112131415161718192021222324252627282930
2?•??????5???2??????????13?????4
8???????•3?15???2?????22??33????4?
975657463•766554574573653532542
24?133210?13?333?1313??22317?33171827?•?3312301089
26??17??3??3?18?2?19?????19??33?•????
27????492114?2?22?10?10?????2??12??•?88
3084274?4??2?44??622??8?23??89??8??•

2 Tiles

3 Tiles

4 Tiles

5 Tiles

6 Tiles

7 Tiles

8 Tiles

10 Tiles

12 Tiles

13 Tiles

14 Tiles

15 Tiles

17 Tiles

18 Tiles

19 Tiles

21 Tiles

22 Tiles

23 Tiles

27 Tiles

30 Tiles

32 Tiles

33 Tiles

49 Tiles

89 Tiles

Last revised 2025-10-18.

Back to Polyabolo/Polytan and Polyfett Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]