Tiling a Rectangle with A Scaled Tetrabolo and a Scaled Pentabolo

Introduction

A tetrabolo or tetratan is a plane figure formed by joining four equal isosceles right triangles at their legs or hypotenuses. A pentabolo or pentatan is a plane figure formed by joining five equal isosceles right triangles at their legs or hypotenuses.

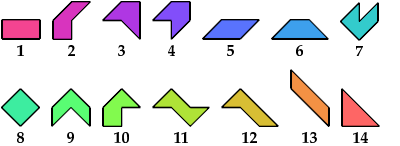
Here are the 14 tetraboloes:

Here are the 30 pentaboloes:

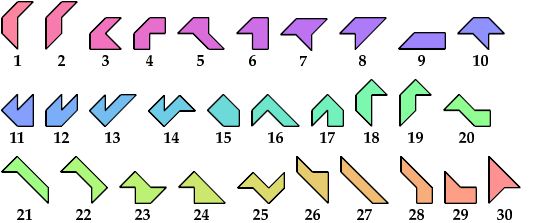
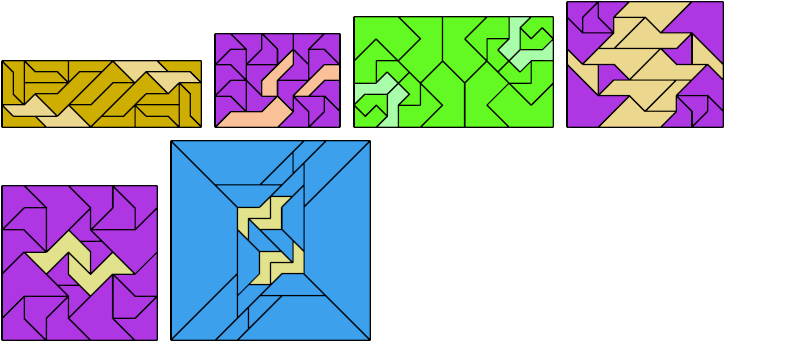
A scaled polyabolo is one that may be used at various scale factors:

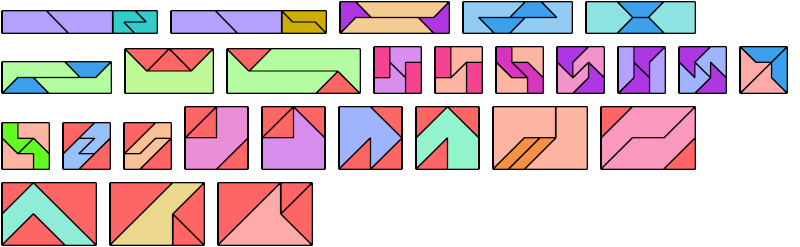
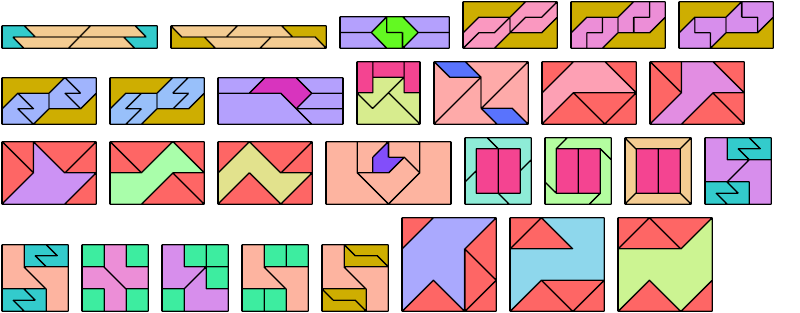
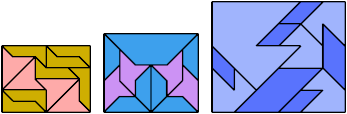
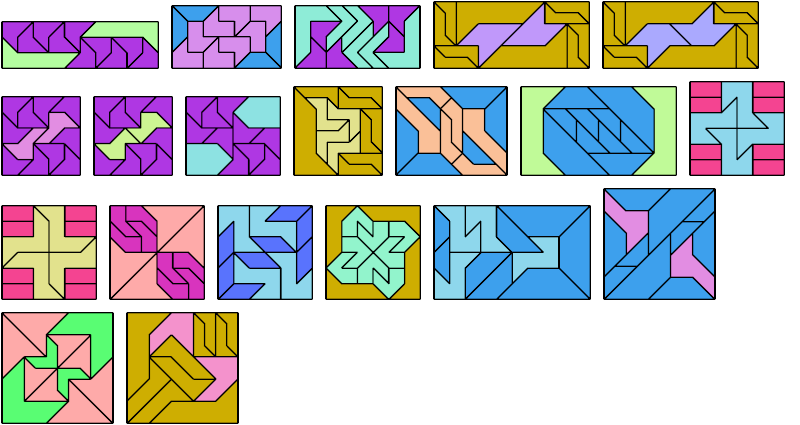
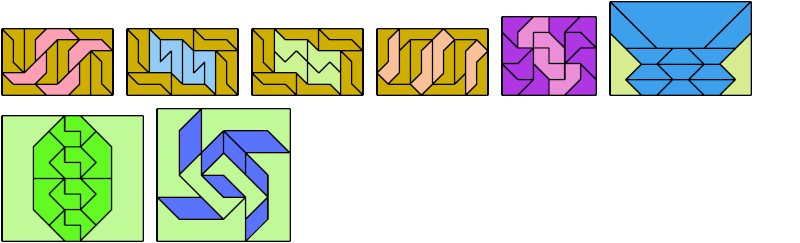
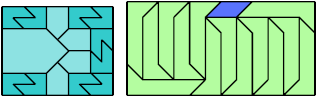
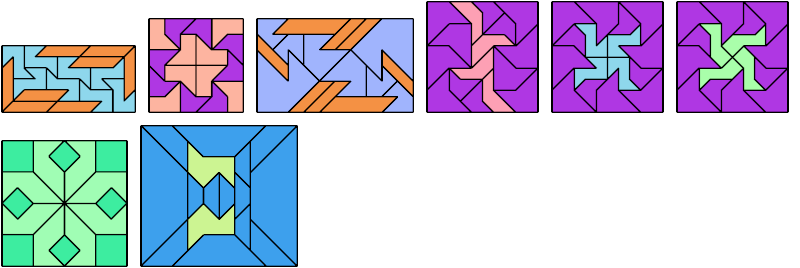
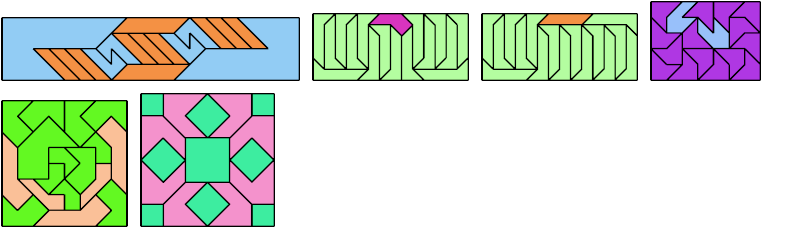
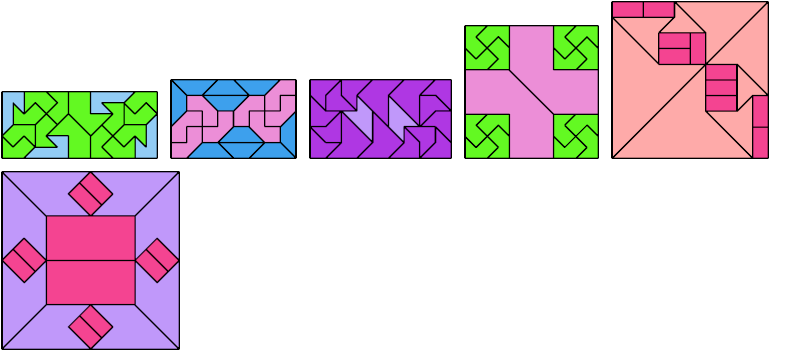
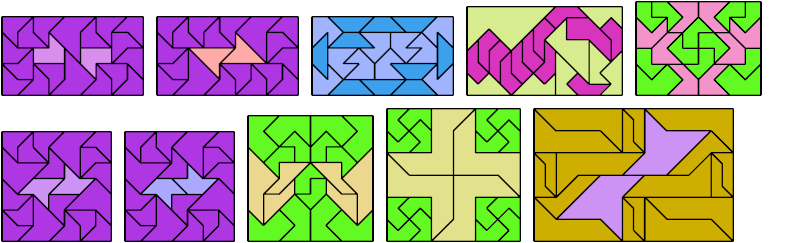
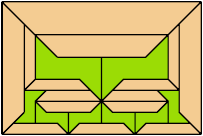
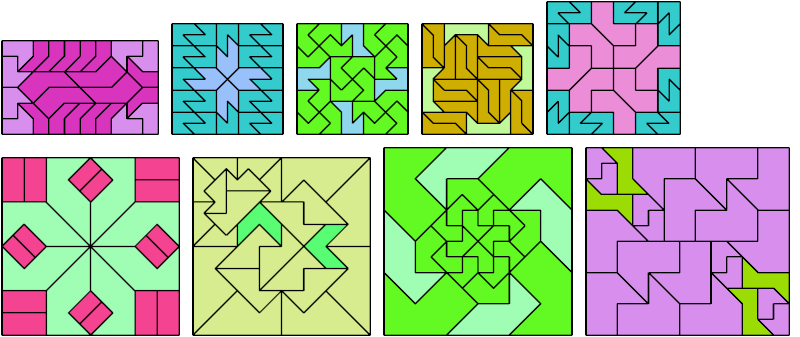
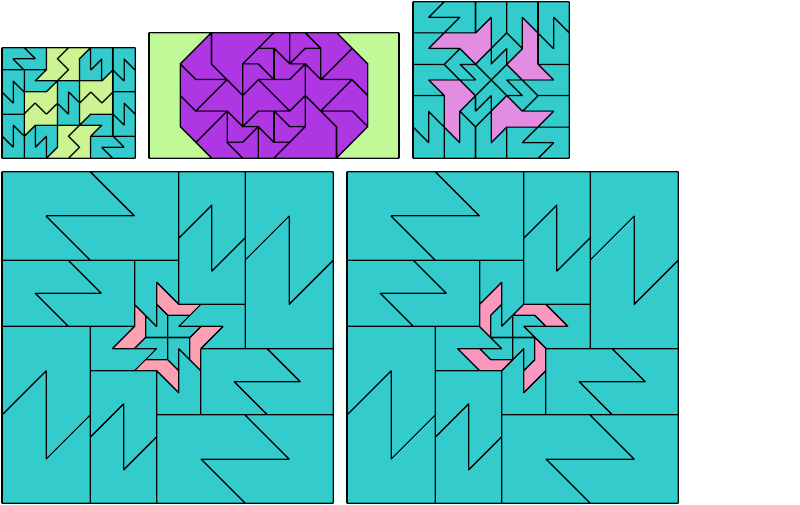
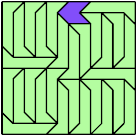
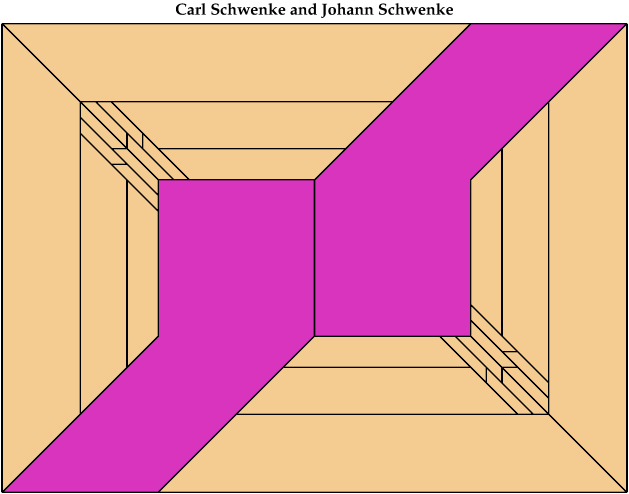
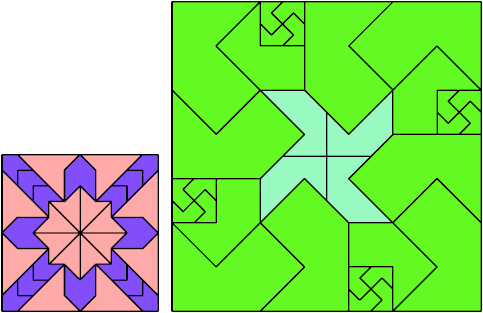
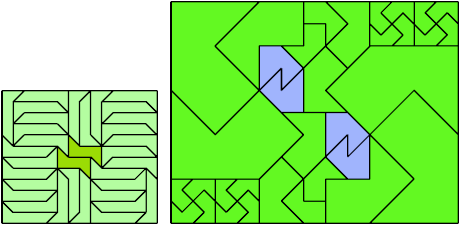
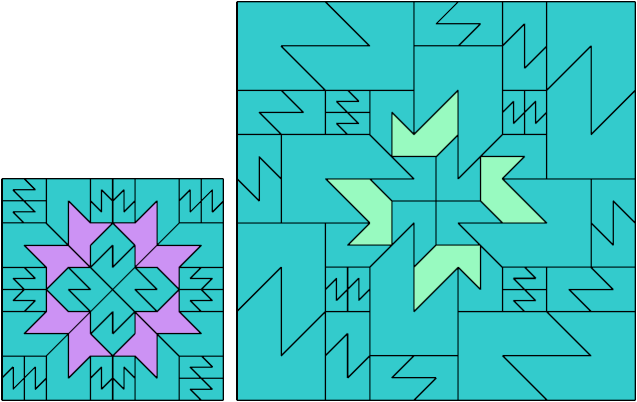
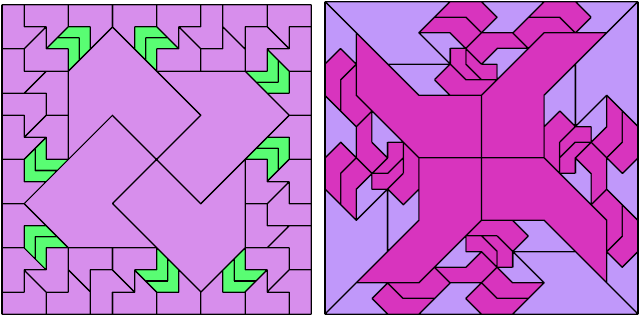
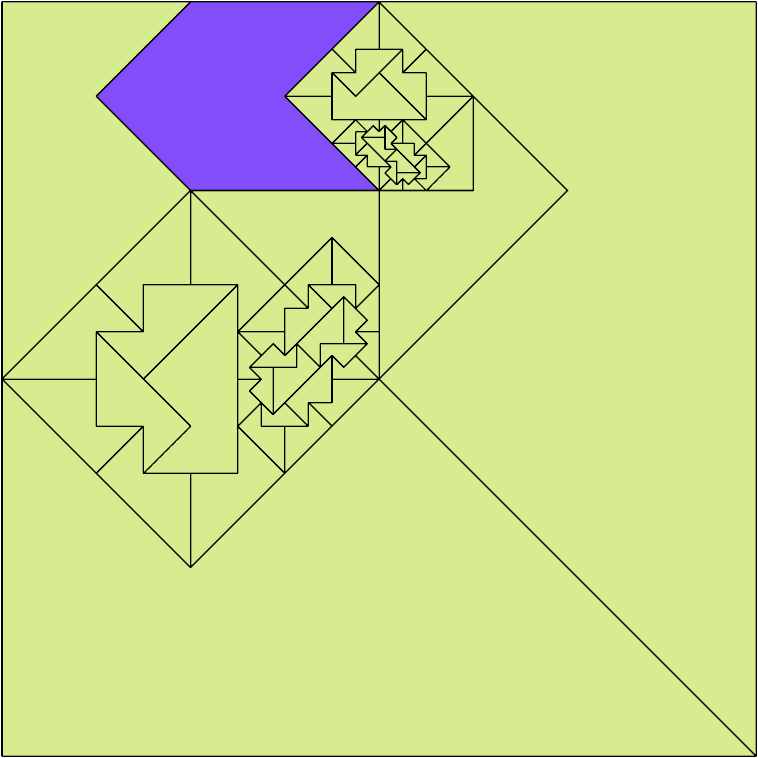
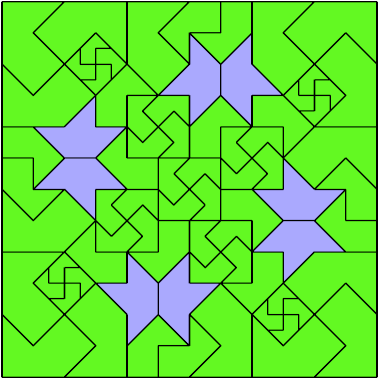
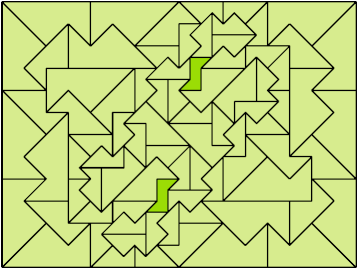
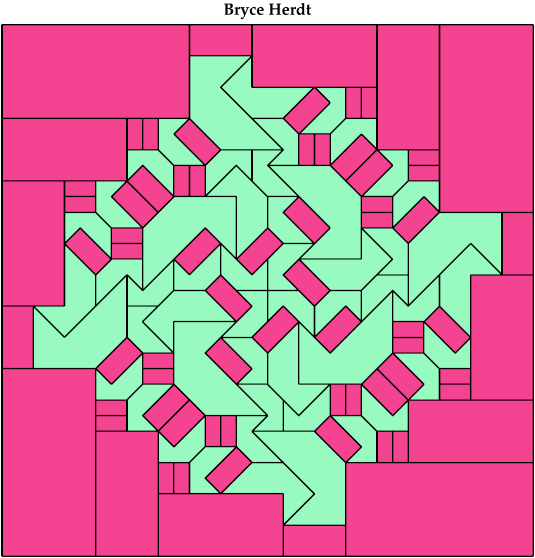
Here I show a rectangle tiled by a scaled tetrabolo and a scaled pentabolo, using at least one copy of each and as few total copies as is known to be possible. If you find a solution with fewer tiles or solve an unsolved case, please write.

Bryce Herdt improved several solutions. Carl Schwenke and Johann Schwenke solved unsolved cases and improved several solutions.

See also

  • Tiling a Rectangle with Two Scaled Pentaboloes
  • Tiling a Rectangle with a Scaled Triabolo and a Scaled Pentabolo

    • Table

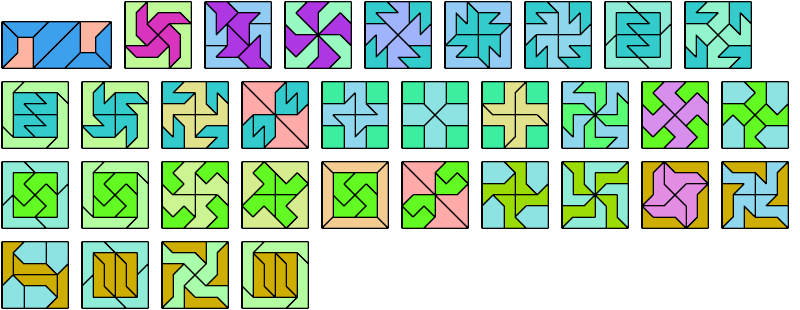
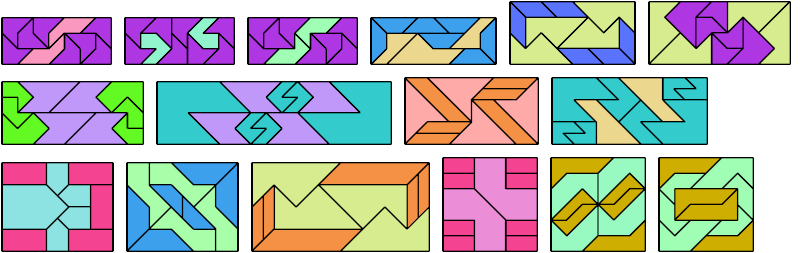
      123456789101112131415161718192021222324252627282930
    1? ? 26 10 ? 4 ? 18 3 ? ? ? ? 12 10 6 ? 124 14 ? 6 ? ? 6 12 ? 6 ? 4 14
    2? ? ? ? ? 24 ? 60 6 ? ? ? ? ? ? 144 ? ? 104 ? 17 8 ? 20 ? ? 30 ? 4 12
    316 10 4 14 12 20 20 18 4 20 4 17 8 16 12 12 10 8 10 16 12 28 12 10 22 22 4 22 16 20
    4? ? ? ? ? 52 ? ? 5 ? ? ? ? ? ? ? ? ? ? ? 29 ? ? 69 ? ? ? ? 6 32
    5? ? ? ? ? 44 ? ? 3 ? 8 ? 12 12 ? ? ? ? ? ? 15 12 ? 10 ? ? ? ? 3 6
    6? ? ? 18 12 12 11 ? 3 ? 20 ? 4 10 4 ? 26 ? ? 10 4 6 16 10 22 10 ? 12 6 4
    728 28 36 18 28 6 56 10 4 72 8 20 8 8 15 8 8 48 22 ? 8 8 24 7 8 10 6 ? 6 8
    8? ? 17 6 ? 6 ? 13 3 ? ? ? ? 8 8 5 ? 128 16 ? 5 ? ? 5 8 ? 5 ? 6 17
    9? ? ? ? ? 60 ? ? 5 ? 48 ? ? 8 ? ? ? ? ? ? 26 ? ? 24 ? ? ? ? 5 12
    1044 40 20 18 48 8 48 10 6 76 34 40 18 20 8 8 44 32 24 22 8 12 8 7 20 20 8 17 4 8
    11? ? ? ? ? 24 ? ? 3 ? ? ? ? ? 8 8 ? ? ? ? 34 ? ? 82 ? ? 23 ? ? ?
    1214 6 12 6 8 6 20 12 4 12 6 6 14 8 8 8 12 10 10 8 8 24 14 9 12 22 6 14 6 11
    13? ? ? ? ? 48 ? ? 3 ? 12 ? 16 14 ? ? ? ? ? ? 16 16 ? 10 ? ? ? ? 4 8
    146 4 3 4 6 4 6 3 2 6 4 4 3 6 3 4 4 5 3 6 4 4 6 3 6 4 3 4 3 4
      123456789101112131415161718192021222324252627282930

    Navigation

    Tiles
    2 3 4 5 6 7 8 9 10
    11 12 13 14 15 16 17 18 20
    22 23 24 26 28 29 30 32 34
    36 40 44 48 52 56 60 69 72
    76 82 104 124 128 144

    2 Tiles

    3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    7 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    11 Tiles

    12 Tiles

    13 Tiles

    14 Tiles

    15 Tiles

    16 Tiles

    17 Tiles

    18 Tiles

    20 Tiles

    22 Tiles

    23 Tiles

    24 Tiles

    26 Tiles

    28 Tiles

    29 Tiles

    30 Tiles

    32 Tiles

    34 Tiles

    36 Tiles

    40 Tiles

    44 Tiles

    48 Tiles

    52 Tiles

    56 Tiles

    60 Tiles

    69 Tiles

    72 Tiles

    76 Tiles

    82 Tiles

    104 Tiles

    124 Tiles

    128 Tiles

    144 Tiles

    Last revised 2025-10-31.

    Back to Polyabolo/Polytan and Polyfett Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]