Tiling a Rectangle with A Scaled Triabolo and a Scaled Pentabolo

Introduction

A triabolo or tritan is a plane figure formed by joining three equal isosceles right triangles at their legs or hypotenuses. A pentabolo or pentatan is a plane figure formed by joining five equal isosceles right triangles at their legs or hypotenuses.

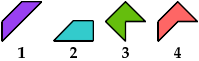
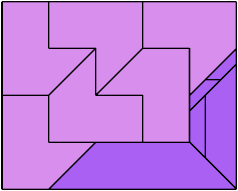
Here are the 4 triaboloes:

Here are the 30 pentaboloes:

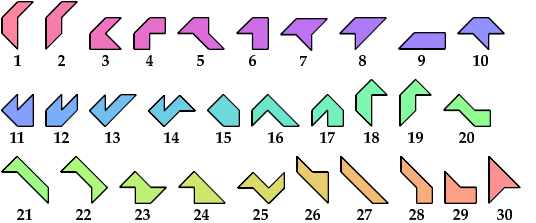
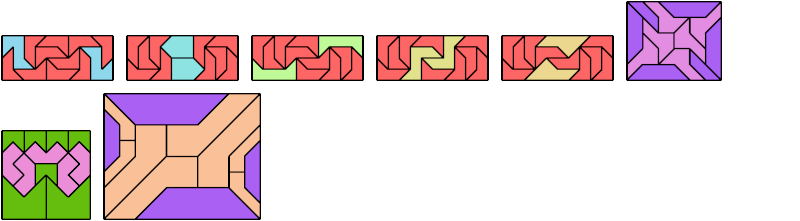
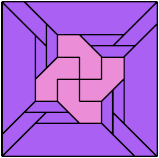
A scaled polyabolo is one that may be used at various scale factors:

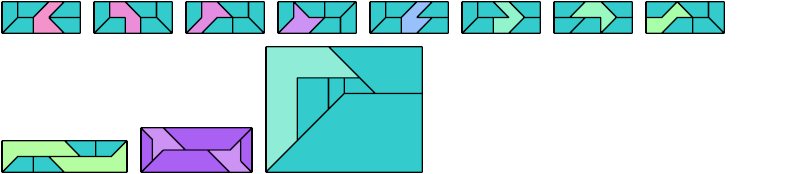
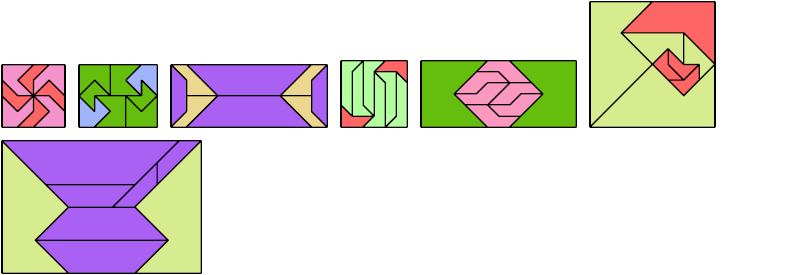
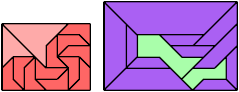
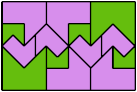
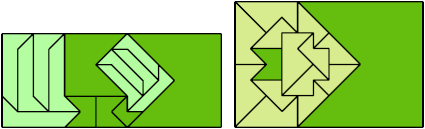
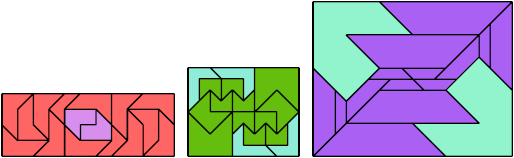
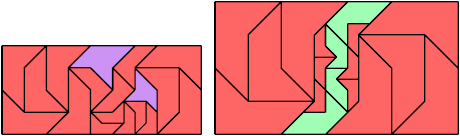
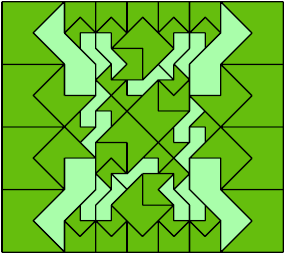
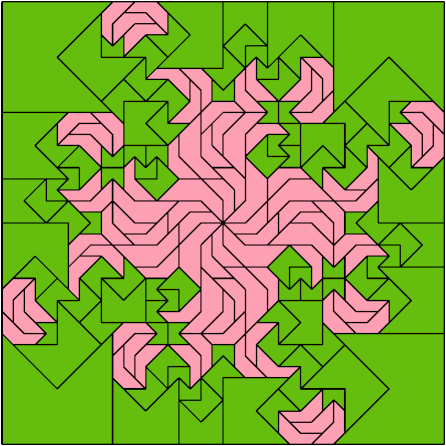
Here I show a rectangle tiled by a scaled triabolo and a scaled pentabolo, using at least one copy of each and as few total copies as is known to be possible. If you find a solution with fewer tiles or solve an unsolved case, please write.

See also

  • Tiling a Rectangle with Two Scaled Pentaboloes
  • Tiling a Rectangle with a Scaled Tetrabolo and a Scaled Pentabolo

    • Table

      123456789101112131415161718192021222324252627282930
    1? ? ? 20 12 11 6 ? 3 ? 10 ? 4 10 4 ? 16 ? ? 13 4 2 10 8 21 8 ? 12 3 4
    27 5 6 6 6 3 6 4 2 7 5 6 3 5 3 6 6 6 5 6 6 3 7 3 7 3 3 3 2 3
    3196 8 28 12 54 14 ? ? 3 ? 8 4 ? ? 2 16 4 7 22 66 15 ? ? 15 22 28 4 4 5 40
    410 10 8 19 10 16 18 10 4 10 4 10 2 12 12 10 10 4 18 10 8 12 10 8 12 12 4 10 7 13
      123456789101112131415161718192021222324252627282930

    Navigation

    Tiles
    2 3 4 5 6 7 8 10 11
    12 13 14 15 16 18 19 20 21
    22 28 40 54 66 196

    2 Tiles

    3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    7 Tiles

    8 Tiles

    10 Tiles

    11 Tiles

    12 Tiles

    13 Tiles

    14 Tiles

    15 Tiles

    16 Tiles

    18 Tiles

    19 Tiles

    20 Tiles

    21 Tiles

    22 Tiles

    28 Tiles

    40 Tiles

    54 Tiles

    66 Tiles

    196 Tiles

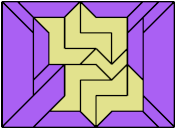
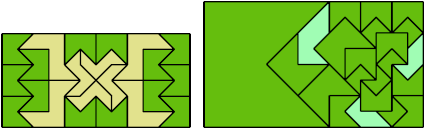
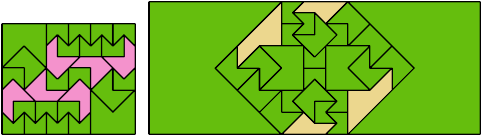
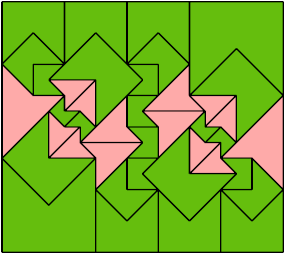
    Last revised 2025-10-31.

    Back to Polyabolo/Polytan and Polyfett Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]