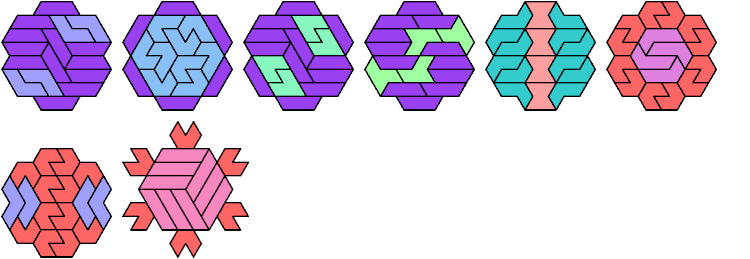Baiocchi Figures for Pentiamond-Hexiamond Pairs
Introduction
A pentiamond is a plane figure formed by joining 5 equilateral
triangles edge to edge.
A hexiamond is a plane figure formed by joining 6 equilateral
triangles edge to edge.
Here I show the smallest polyiamond with
full symmetry that can be tiled by a pentiamond and a hexiamond,
using at least one copy of each.
The solutions shown are not necessarily uniquely minimal.
See also Baiocchi Figures
for Pentiamond-Heptiamond Pairs.
Basic Solutions
| 5I+6A : 66 | 5J+6A : 54 | 5Q+6A : 66 | 5U+6A : 36 |
 |  |  |  |
| 5I+6E : 66 | 5J+6E : 42 | 5Q+6E : 66 | 5U+6E : 42 |
 |  |  |  |
| 5I+6F : 48 | 5J+6F : 48 | 5Q+6F : 54 | 5U+6F : 48 |
 |  |  |  |
| 5I+6H : 48 | 5J+6H : 42 | 5Q+6H : 66 | 5U+6H : 48 |
 |  |  |  |
| 5I+6I : 54 | 5J+6I : 48 | 5Q+6I : 42 | 5U+6I : 66 |
 |  |  |  |
| 5I+6L : 48 | 5J+6L : 42 | 5Q+6L : 48 | 5U+6L : 66 |
 |  |  |  |
| 5I+6O : 48 | 5J+6O : 42 | 5Q+6O : 36 | 5U+6O : 36 |
 |  |  |  |
| 5I+6P : 54 | 5J+6P : 48 | 5Q+6P : 54 | 5U+6P : 66 |
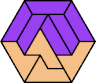 | 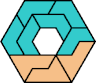 |  |  |
| 5I+6S : 66 | 5J+6S : 42 | 5Q+6S : 48 | 5U+6S : 66 |
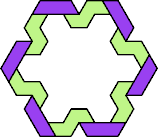 |  |  | 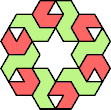 |
| 5I+6U : 66 | 5J+6U : 42 | 5Q+6U : 48 | 5U+6U : 48 |
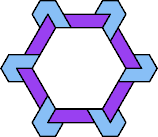 |  |  |  |
| 5I+6V : 42 | 5J+6V : 48 | 5Q+6V : 48 | 5U+6V : 48 |
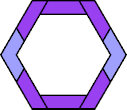 |  | 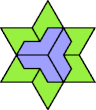 |  |
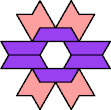
| 5I+6X : 54 | 5J+6X : 66 | 5Q+6X : 66 | 5U+6X : 48 |
 | 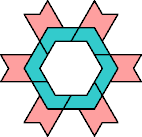 |  |  |
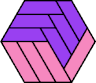
Holeless Variants
54 Cells

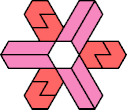
60 Cells
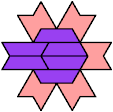
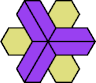
72 Cells

78 Cells

84 Cells
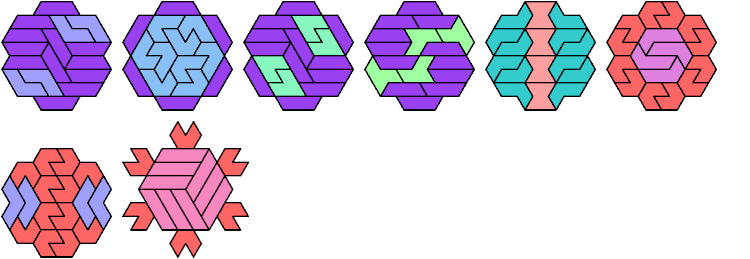
96 Cells
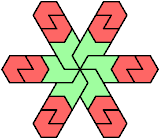
114 Cells
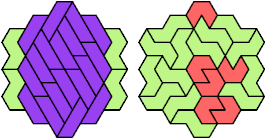
No Holeless Solution

Last revised 2024-11-13.
Back to Baiocchi Figures
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]