Baiocchi Figures for Pentiamond-Heptiamond Pairs
Introduction
A pentiamond is a plane figure formed by joining 5 equilateral
triangles edge to edge.
A heptiamond is a plane figure formed by joining 7 equilateral
triangles edge to edge.
Here I show the smallest polyiamond with
full symmetry that can be tiled by a pentiamond and a heptiamond,
using at least one copy of each.
The solutions shown are not necessarily uniquely minimal.
See also Baiocchi
Figures for Pentiamond-Hexiamond Pairs.
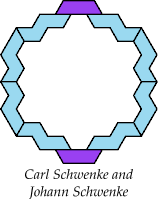
Carl Schwenke and Johann Schwenke contributed solutions.
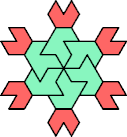
Basic Solutions
| 5I+7A : 72 | 5J+7A : 66 | 5Q+7A : 36 | 5U+7A : 72 |
 |  |  |  |
| 5I+7B : 54 | 5J+7B : 24 | 5Q+7B : 54 | 5U+7B : 66 |
 |  |  |  |
| 5I+7C : 24 | 5J+7C : 24 | 5Q+7C : 24 | 5U+7C : 24 |
 |  |  |  |
| 5I+7D : 24 | 5J+7D : 54 | 5Q+7D : 24 | 5U+7D : 36 |
 |  |  |  |
| 5I+7E : 72 | 5J+7E : 54 | 5Q+7E : 36 | 5U+7E : 72 |
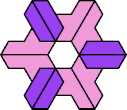 |  |  |  |
| 5I+7F : 36 | 5J+7F : 36 | 5Q+7F : 72 | 5U+7F : 24 |
 |  |  |  |
| 5I+7G : 48 | 5J+7G : 24 | 5Q+7G : 36 | 5U+7G : 72 |
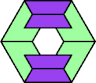 |  |  | 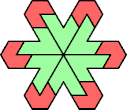 |
| 5I+7H : 54 | 5J+7H : 54 | 5Q+7H : 36 | 5U+7H : 66 |
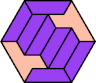 | 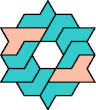 |  | 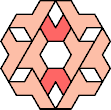 |
| 5I+7I : 24 | 5J+7I : 54 | 5Q+7I : 48 | 5U+7I : 72 |
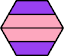 | 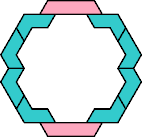 | 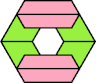 | 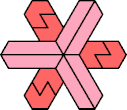 |
| 5I+7J : 24 | 5J+7J : 24 | 5Q+7J : 48 | 5U+7J : 72 |
 |  |  | 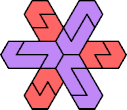 |
| 5I+7K : 72 | 5J+7K : 36 | 5Q+7K : 54 | 5U+7K : 72 |
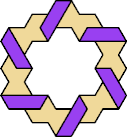 |  |  |  |
| 5I+7L : 72 | 5J+7L : 54 | 5Q+7L : 48 | 5U+7L : 72 |
 |  |  |  |
| 5I+7M : 72 | 5J+7M : 54 | 5Q+7M : 54 | 5U+7M : 66 |
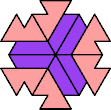 | 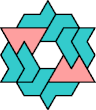 |  |  |
| 5I+7N : 66 | 5J+7N : 54 | 5Q+7N : 24 | 5U+7N : 66 |
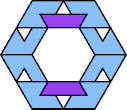 |  |  | 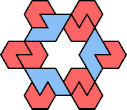 |
| 5I+7P : 72 | 5J+7P : 54 | 5Q+7P : 72 | 5U+7P : 72 |
 |  |  | 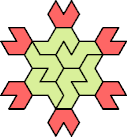 |
| 5I+7Q : 36 | 5J+7Q : 36 | 5Q+7Q : 54 | 5U+7Q : 72 |
 |  |  | 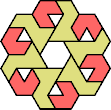 |
| 5I+7R : 24 | 5J+7R : 72 | 5Q+7R : 48 | 5U+7R : 72 |
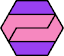 |  | 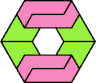 |  |
| 5I+7S : 66 | 5J+7S : 54 | 5Q+7S : 36 | 5U+7S : 72 |
 |  |  |  |
| 5I+7T : 72 | 5J+7T : 24 | 5Q+7T : 54 | 5U+7T : 72 |
 |  |  | 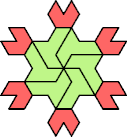 |
| 5I+7U : 72 | 5J+7U : 54 | 5Q+7U : 54 | 5U+7U : 72 |
 | 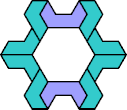 |  | 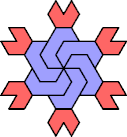 |
| 5I+7V : 54 | 5J+7V : 54 | 5Q+7V : 54 | 5U+7V : 66 |
 |  |  |  |
| 5I+7X : 72 | 5J+7X : 66 | 5Q+7X : 96 | 5U+7X : 72 |
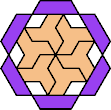 |  | 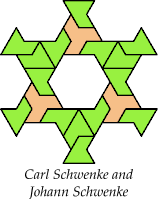 | 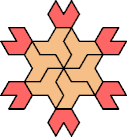 |
| 5I+7Y : 54 | 5J+7Y : 54 | 5Q+7Y : 72 | 5U+7Y : 24 |
 |  |  |  |
| 5I+7Z : 72 | 5J+7Z : 54 | 5Q+7Z : 36 | 5U+7Z : 72 |
 |  |  |  |
Holeless Variants
54 Cells
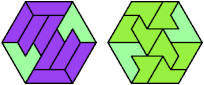
60 Cells

66 Cells

72 Cells
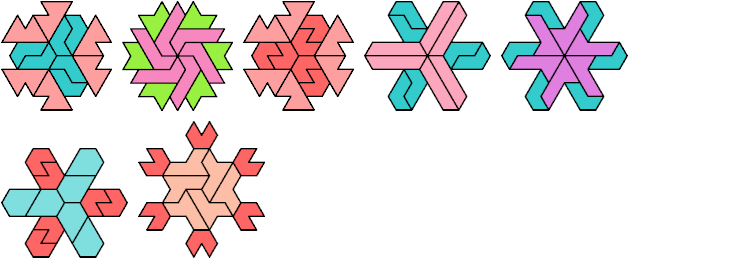
78 Cells
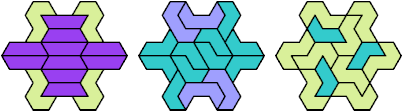
84 Cells
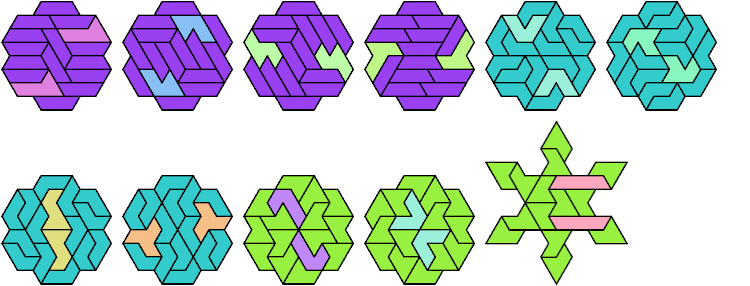
90 Cells
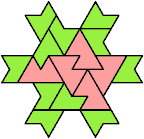
96 Cells
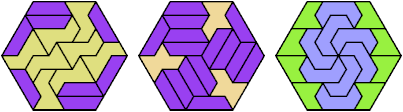
102 Cells
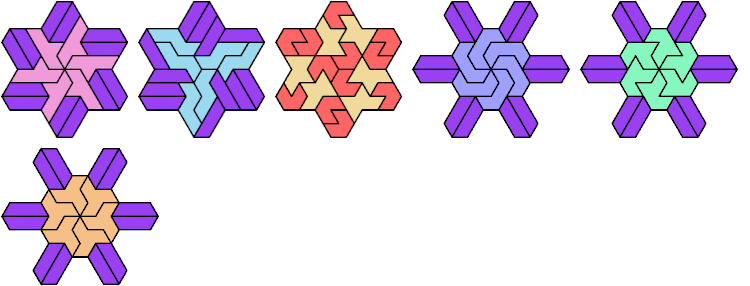
132 Cells
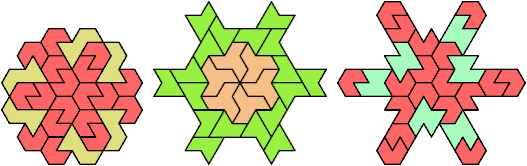
168 Cells

174 Cells
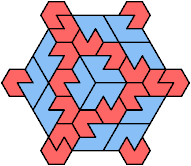
No Holeless Solution
Last revised 2025-03-12.
Back to Baiocchi Figures
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]