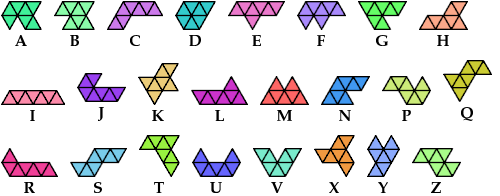
A heptiamond is a plane figure formed by joining 7 equal equilateral triangles edge to edge. There are 24 heptiamonds:
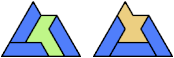
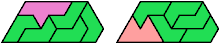
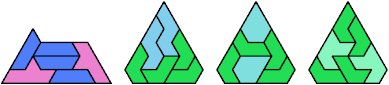
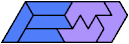
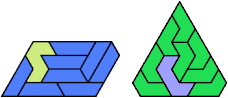
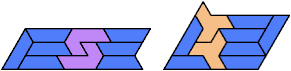
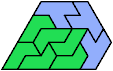
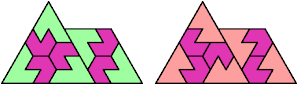
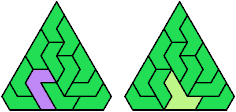
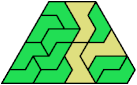
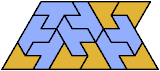
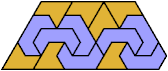
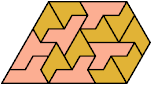
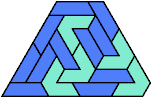
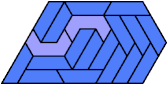
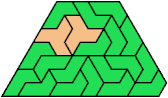
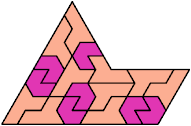
Here I show the smallest known pentagonal (five-sided) polyiamonds that can be formed by copies of a pentiamond and a heptiamond, using at least one of each. If you find a smaller solution, please write.
See also
| 7A | 7B | 7C | 7D | 7E | 7F | 7G | 7H | 7I | 7J | 7K | 7L | 7M | 7N | 7P | 7Q | 7R | 7S | 7T | 7U | 7V | 7X | 7Y | 7Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5I | 37 | 17 | 17 | 17 | 34 | 41 | 17 | 19 | 17 | 49 | 22 | 12 | 12 | 29 | 47 | 17 | 37 | 31 | 22 | 99 | 90 | 49 | 37 | 39 |
| 5J | 34 | 36 | 39 | 34 | 32 | 17 | 24 | 17 | 29 | 62 | 39 | 17 | 32 | 36 | 39 | 71 | 29 | 34 | 62 | 47 | 39 | 104 | 51 | 69 |
| 5Q | 36 | 109 | 36 | 17 | ? | 17 | 17 | 87 | 12 | 17 | ? | 31 | 12 | 17 | 17 | ? | 17 | ? | ? | 84 | 36 | ? | 79 | 17 |
| 5U | ? | ? | ? | ? | 189 | ? | 60 | 105 | 19 | ? | ? | 17 | 60 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |

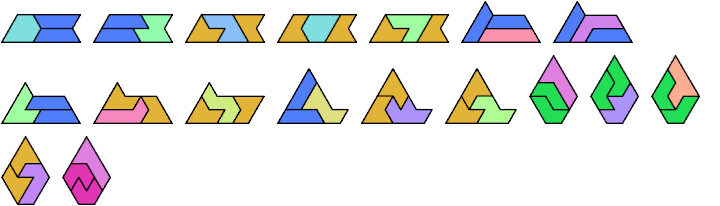



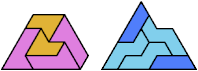






Last revised 2025-03-08.