
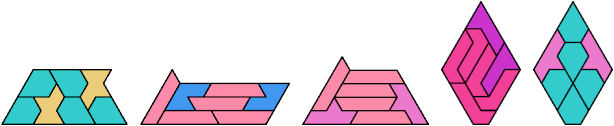
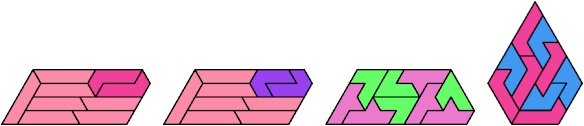
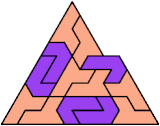
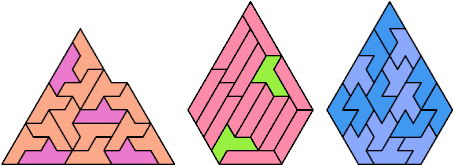
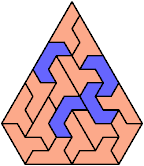
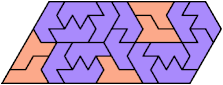
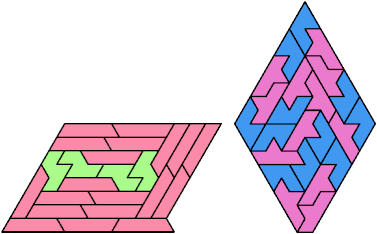
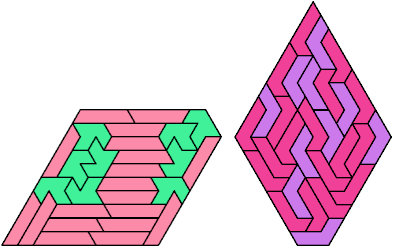
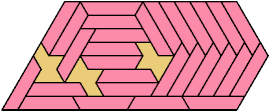
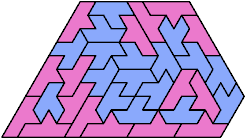
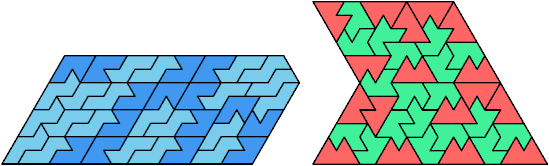
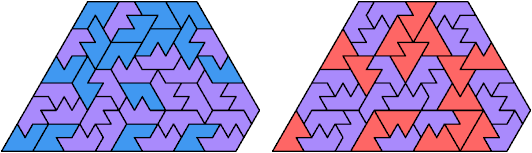
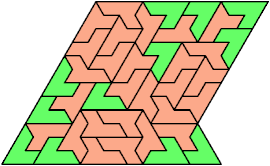
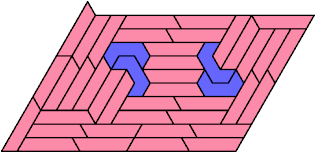
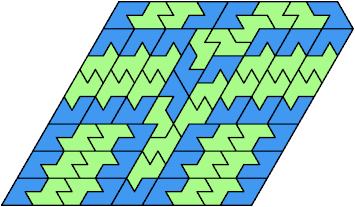
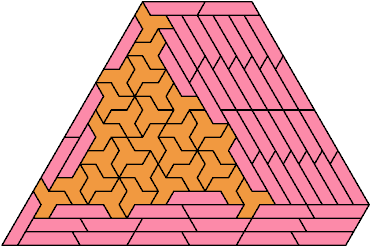
Here I show the smallest known pentagonal (five-sided) polyiamonds that can be formed by copies of two heptiamonds, using at least one of each. If you find a smaller solution, please write.
See also
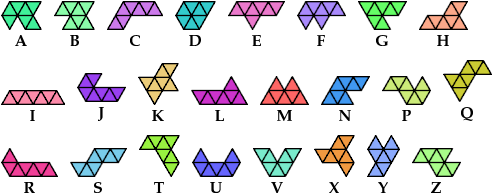
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | ? | ? | ? | 8 | ? | ? | ? | 28 | ? | ? | 4 | 36 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| B | ? | * | ? | 3 | ? | ? | 8 | ? | 3 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| C | ? | ? | * | 4 | 8 | ? | ? | ? | 4 | ? | ? | 26 | ? | ? | ? | ? | 28 | ? | ? | ? | ? | ? | ? | ? |
| D | ? | 3 | 4 | * | 7 | ? | ? | 3 | 3 | ? | 7 | 2 | ? | ? | ? | ? | 2 | ? | ? | 2 | ? | ? | ? | ? |
| E | 8 | ? | 8 | 7 | * | ? | 9 | 16 | 7 | ? | ? | ? | ? | 23 | ? | ? | 25 | ? | ? | ? | 2 | ? | 33 | ? |
| F | ? | ? | ? | ? | ? | * | 2 | 20 | 8 | ? | ? | 5 | 38 | 38 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| G | ? | 8 | ? | ? | 9 | 2 | * | 39 | 3 | ? | 4 | 6 | 2 | ? | ? | ? | 8 | 6 | ? | ? | ? | ? | 3 | 3 |
| H | ? | ? | ? | 3 | 16 | 20 | 39 | * | 4 | 13 | ? | ? | ? | ? | ? | ? | 12 | ? | ? | 18 | ? | ? | ? | ? |
| I | 28 | 3 | 4 | 3 | 7 | 8 | 3 | 4 | * | 9 | 32 | 2 | 2 | 7 | 12 | 4 | 9 | 6 | 16 | 43 | ? | 81 | 12 | 23 |
| J | ? | ? | ? | ? | ? | ? | ? | 13 | 9 | * | ? | 4 | 2 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| K | ? | ? | ? | 7 | ? | ? | 4 | ? | 32 | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| L | 4 | ? | 26 | 2 | ? | 5 | 6 | ? | 2 | 4 | ? | * | ? | ? | ? | ? | 7 | ? | ? | ? | ? | ? | ? | ? |
| M | 36 | ? | ? | ? | ? | 38 | 2 | ? | 2 | 2 | ? | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| N | ? | ? | ? | ? | 23 | 38 | ? | ? | 7 | ? | ? | ? | ? | * | ? | ? | 9 | 36 | ? | ? | ? | ? | 16 | 68 |
| P | ? | ? | ? | ? | ? | ? | ? | ? | 12 | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| Q | ? | ? | ? | ? | ? | ? | ? | ? | 4 | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? | ? | ? | ? |
| R | ? | ? | 28 | 2 | 25 | ? | 8 | 12 | 9 | ? | ? | 7 | ? | 9 | ? | ? | * | 41 | ? | ? | ? | ? | ? | ? |
| S | ? | ? | ? | ? | ? | ? | 6 | ? | 6 | ? | ? | ? | ? | 36 | ? | ? | 41 | * | ? | ? | ? | ? | ? | ? |
| T | ? | ? | ? | ? | ? | ? | ? | ? | 16 | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? |
| U | ? | ? | ? | 2 | ? | ? | ? | 18 | 43 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? |
| V | ? | ? | ? | ? | 2 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? |
| X | ? | ? | ? | ? | ? | ? | ? | ? | 81 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? |
| Y | ? | ? | ? | ? | 33 | ? | 3 | ? | 12 | ? | ? | ? | ? | 16 | ? | ? | ? | ? | ? | ? | ? | ? | * | ? |
| Z | ? | ? | ? | ? | ? | ? | 3 | ? | 23 | ? | ? | ? | ? | 68 | ? | ? | ? | ? | ? | ? | ? | ? | ? | * |










Last revised 2025-03-03.