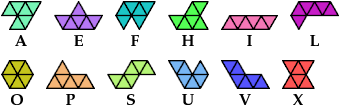

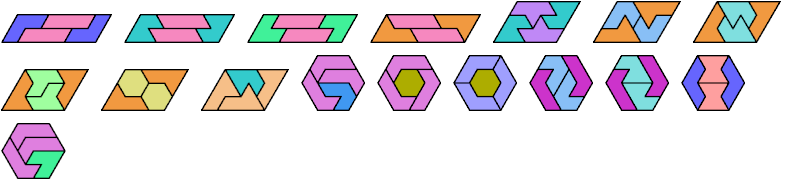
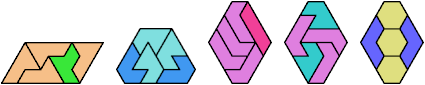
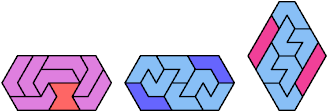
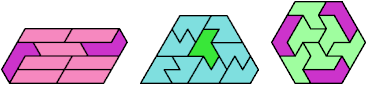
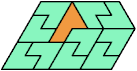
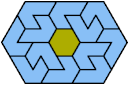
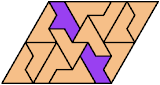
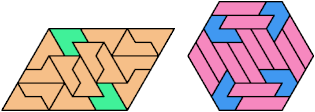
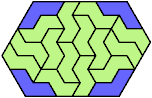
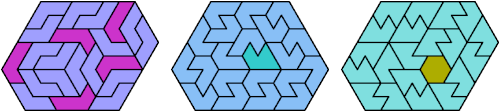
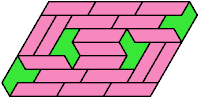
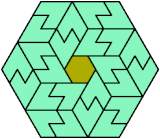
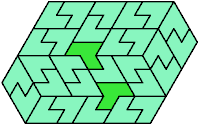
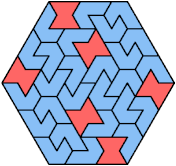
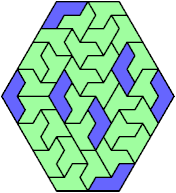
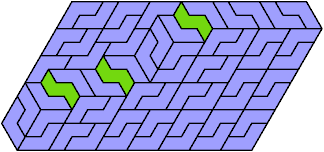
Here I show the smallest known convex shapes that can be formed by copies of two hexiamonds, using at least one of each, and strongly isolating the copies of one so that they do not touch, not even at corners. If you find a smaller solution, please write.
See also
| Isolated Hexiamond | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | L | E | V | U | F | A | H | S | O | P | X | |
| I | * | 9 | ? | 4 | 16 | 4 | 4 | 23 | 17 | 3 | 4 | ? |
| L | 5 | * | 7 | 7 | 4 | 5 | 4 | 7 | 7 | 4 | 6 | 8 |
| E | ? | ? | * | ? | ? | 4 | ? | ? | ? | ? | ? | ? |
| V | 3 | 21 | ? | * | 22 | 12 | 10 | 12 | 61 | 4 | 2 | 22 |
| U | 8 | 4 | 3 | 8 | * | 21 | ? | 7 | 3 | 13 | 4 | 32 |
| F | 3 | 4 | 10 | 10 | 5 | * | 2 | 9 | 7 | 21 | 4 | 17 |
| A | 3 | 22 | ? | 10 | 12 | 2 | * | 30 | ? | 25 | 11 | ? |
| H | 12 | 9 | ? | 35 | 7 | 6 | ? | * | ? | 12 | 4 | ? |
| S | ? | ? | ? | 18 | 3 | ? | ? | ? | * | ? | 3 | ? |
| O | ? | ? | ? | 5 | ? | ? | ? | ? | ? | * | 4 | 3 |
| P | 3 | 6 | 14 | 2 | 3 | 4 | 16 | 5 | 3 | 3 | * | 7 |
| X | ? | ? | ? | 4 | ? | ? | ? | ? | ? | 3 | ? | * |






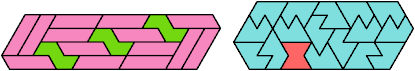

Last revised 2025-05-25.