Tri-Oddities for Heptiamond Pairs

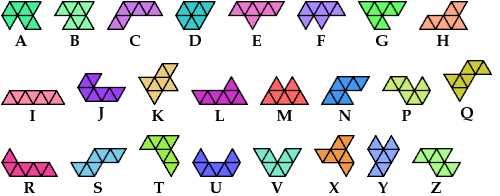
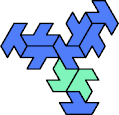
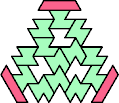
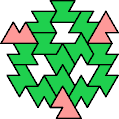
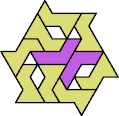
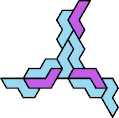
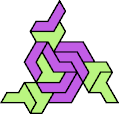
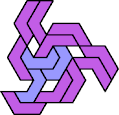
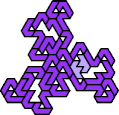
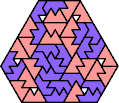
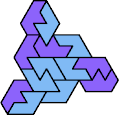
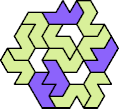
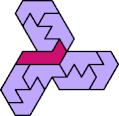
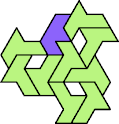
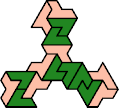
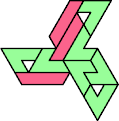
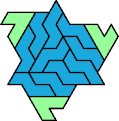
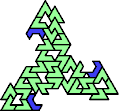
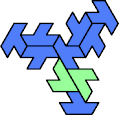
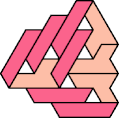
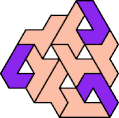
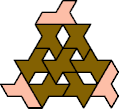
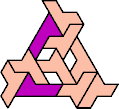
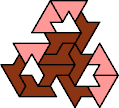
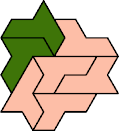
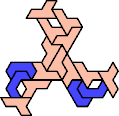
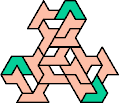
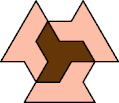
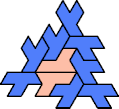
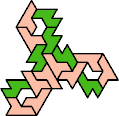
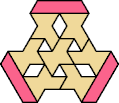
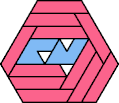
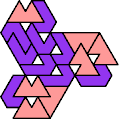
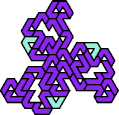
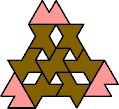
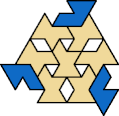
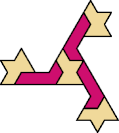
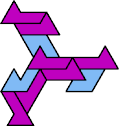
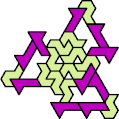
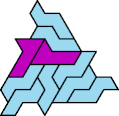
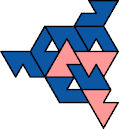
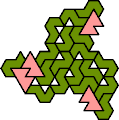
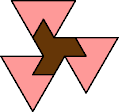
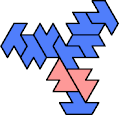
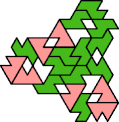
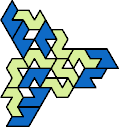
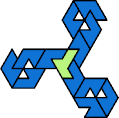
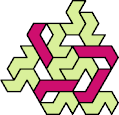
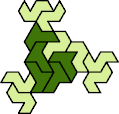
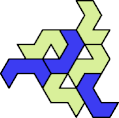
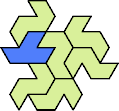
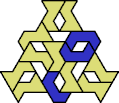
A tri-oddity is an arrangement of copies of a polyform with ternary rotary symmetry or better, using a number of copies that is not a multiple of 3.

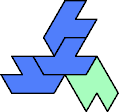
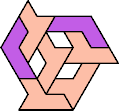
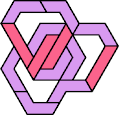
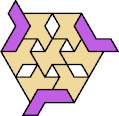
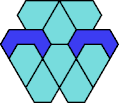
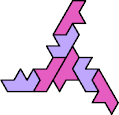
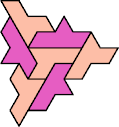
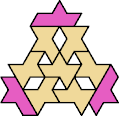
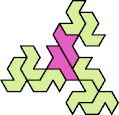
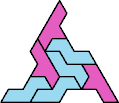
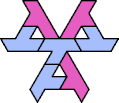
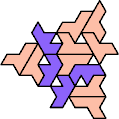
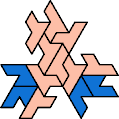
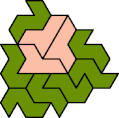
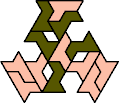
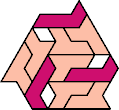
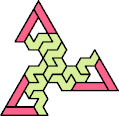
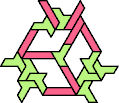
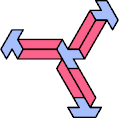
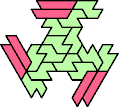
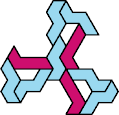
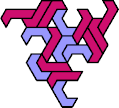
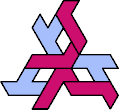
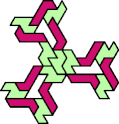
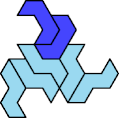
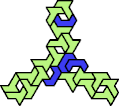
Here I show the smallest known tri-oddities that can be formed by copies of two heptiamonds, using at least one of each. If you find a smaller solution, please write.

See also:

AB 13	AC 13	AD 13	AE 4	AF 10	AG 25
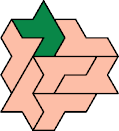
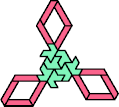
AH 7	AI 19	AJ 10	AK 7	AL 13	AM 22
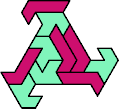
AN 10	AP 10	AQ 10	AR 10	AS 7	AT 7
AU 22	AV 22	AX 4	AY 10	AZ 10	BC 13
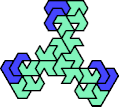
BD 7	BE 7	BF 13	BG 10	BH 10	BI 16
BJ 10	BK 4	BL 16	BM 16	BN 13	BP 10
BQ 16	BR 13	BS 10	BT 16	BU 16	BV 16
BX 4	BY 4	BZ 10	CD 7	CE 7	CF 13
CG 13	CH 7	CI 13	CJ 10	CK 10	CL 10
CM 13	CN 10	CP 7	CQ 10	CR 7	CS 10
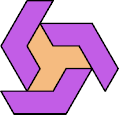
CT 13	CU 13	CV 31	CX 4	CY 10	CZ 10
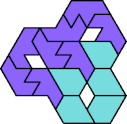
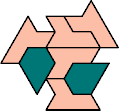
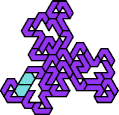
DE 10	DF 13	DG 34	DH 7	DI 10	DJ 37
DK 10	DL 7	DM 28	DN 16	DP 13	DQ 4
DR 10	DS 4	DT 7	DU 10	DV ?	DX 4
DY 10	DZ 10	EF 7	EG 13	EH 7	EI 13
EJ 16	EK 10	EL 16	EM 22	EN 16	EP 10
EQ 13	ER 13	ES 7	ET 10	EU 10	EV 10
EX 4	EY 7	EZ 13	FG 10	FH 13	FI 31
FJ 37	FK 10	FL 10	FM 40	FN 13	FP 13
FQ 10	FR 10	FS 7	FT 10	FU 13	FV ?
FX 4	FY 7	FZ 10	GH 16	GI 10	GJ 13
GK 7	GL 10	GM 31	GN 10	GP 19	GQ 19
GR 10	GS 13	GT 16	GU 34	GV 34	GX 4
GY 10	GZ 13	HI 10	HJ 10	HK 10	HL 10
HM 13	HN 13	HP 10	HQ 13	HR 10	HS 4
HT 7	HU 16	HV 16	HX 4	HY 10	HZ 16
IJ 16	IK 10	IL 10	IM 10	IN 13	IP 16
IQ 13	IR 13	IS 7	IT 19	IU ?	IV 25
IX 4	IY 10	IZ 19	JK 10	JL 13	JM 16
JN 10	JP 7	JQ 13	JR 10	JS 4	JT 10
JU 19	JV 40	JX 4	JY 7	JZ 16	KL 7
KM 10	KN 10	KP 7	KQ 7	KR 7	KS 7
KT 7	KU 10	KV 7	KX 4	KY 4	KZ 10
LM 16	LN 10	LP 22	LQ 13	LR 10	LS 10
LT 13	LU 13	LV ?	LX 4	LY 10	LZ 10
MN 10	MP 22	MQ ?	MR 19	MS 13	MT 25
MU ?	MV ?	MX 4	MY 10	MZ 19	NP 16
NQ 13	NR 19	NS 13	NT 13	NU ?	NV 28
NX 4	NY 10	NZ 10	PQ 10	PR 13	PS 10
PT 13	PU 7	PV 22	PX 4	PY 7	PZ 7
QR 16	QS 7	QT 13	QU 13	QV ?	QX 4
QY 10	QZ 7	RS 10	RT 13	RU 16	RV 16
RX 4	RY 7	RZ 19	ST 7	SU 7	SV 10
SX 4	SY 7	SZ 4	TU 22	TV 19	TX 4
TY 7	TZ 13	UV ?	UX 4	UY 10	UZ 22
VX 4	VY 10	VZ 16	XY 4	XZ 4	YZ 10

Last revised 2025-02-22.