Tiling a Polyomino at Scale 2 with a Pentomino

  • Introduction
  • Table
  • Solutions
  • Holeless Variants

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

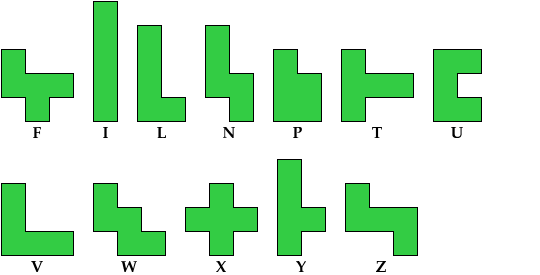
    Here I study the problem of arranging copies of a pentomino to form some polyomino that has been scaled up by a factor of 2.

    See also

  • Tiling a Polyomino at Scale 2 with Two Pentominoes
  • Tiling a Polyomino at Scale 2 with a Tetromino and a Pentomino
  • Tiling a Polyiamond at Scale 2 with Two Hexiamonds
  • Tiling a Polyabolo at Scale 2 with Two Tetraboloes

    • Andrew Bayly and Helmut Postl identified the smallest tilings for the N-pentomino.

    Solutions

    So far as I know, these solutions use as few tiles as possible. They are not necessarily uniquely minimal.

    I-Pentomino

    This tiling has 4 tiles.

    L Pentomino

    These tilings have 4 tiles.

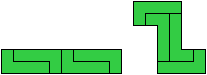
    P Pentomino

    These tilings have 4 tiles.

    V Pentomino

    This tiling has 4 tiles.

    Z Pentomino

    This tiling has 4 tiles.

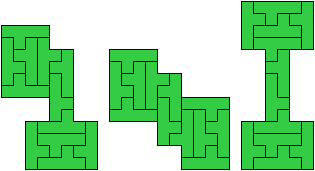
    Y Pentomino

    These tilings have 12 tiles.

    N Pentomino

    These tilings have 64 tiles.

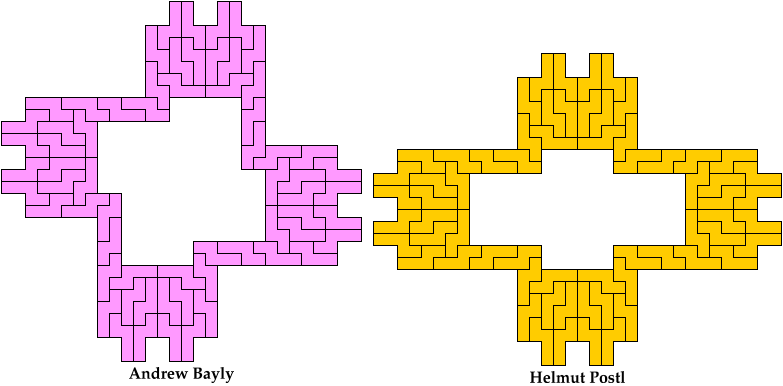
    This holeless solution has 116 tiles.

    Last revised 2025-10-07.

    Back to Polyomino and Polyking Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]