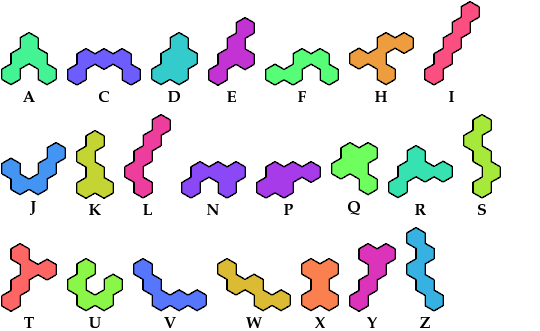

A tetrahex is a polyhex with 4 cells. There are 7 pentahexes, not distinguishing reflections and rotations.

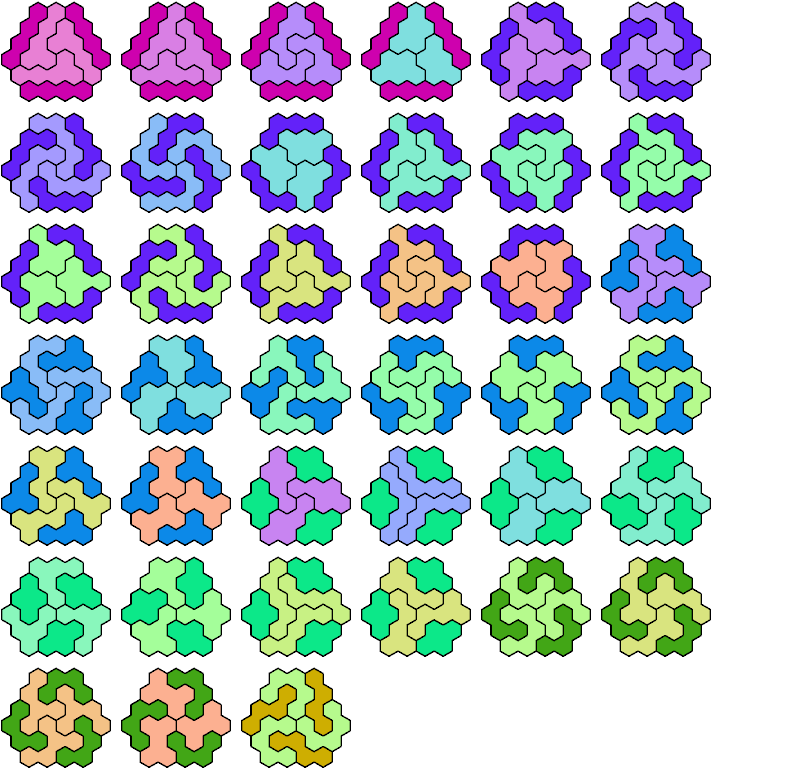
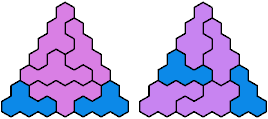
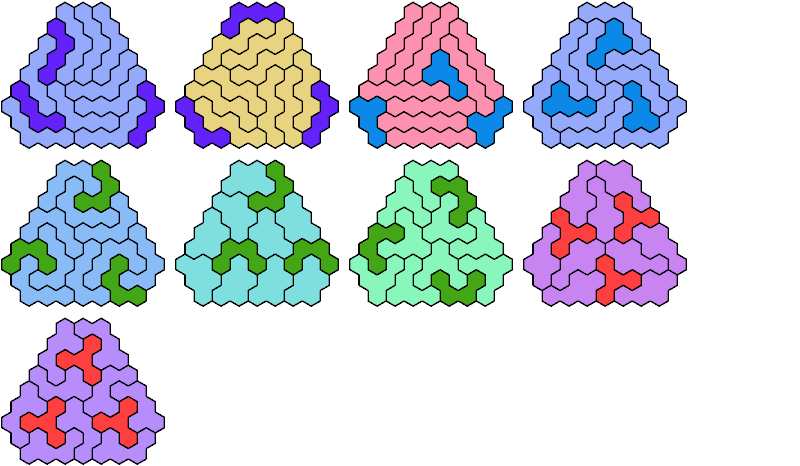
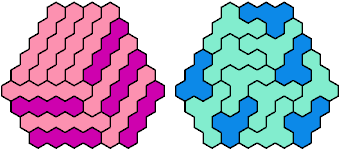
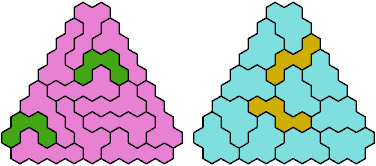
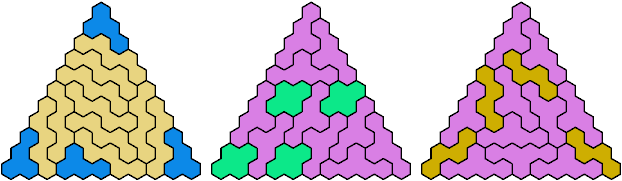
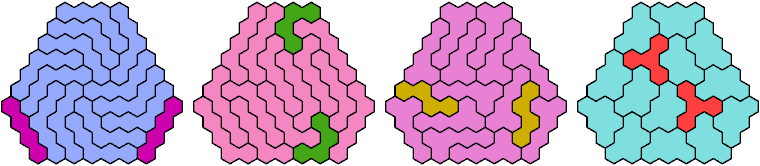
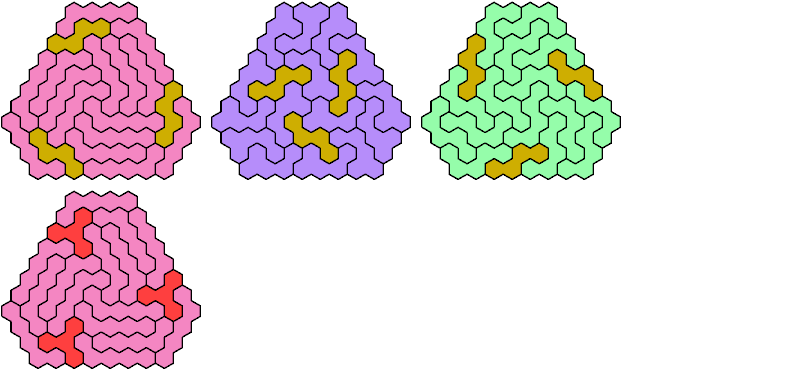
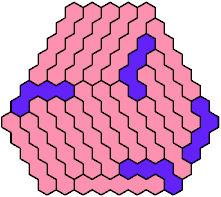
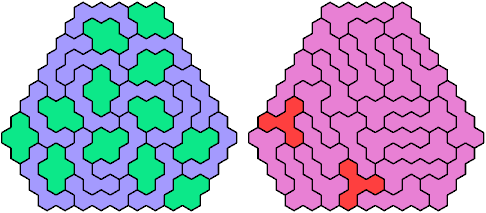
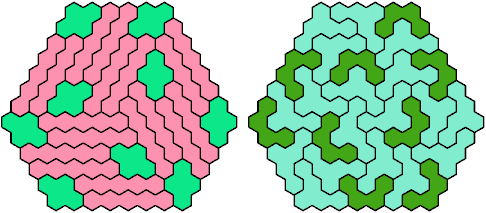
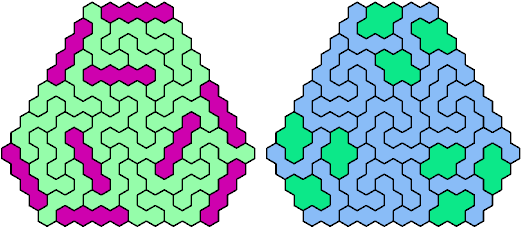
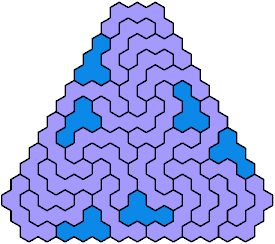
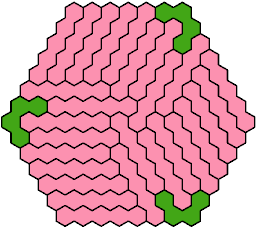
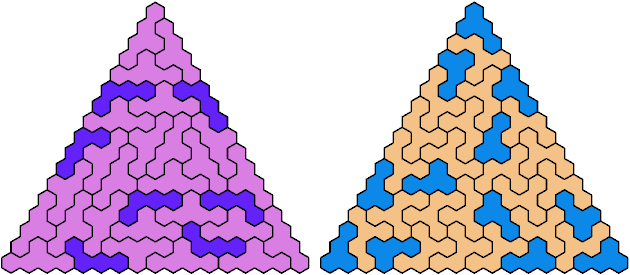
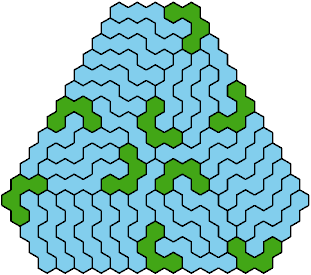
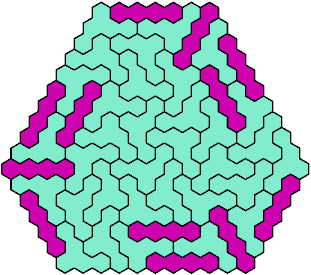
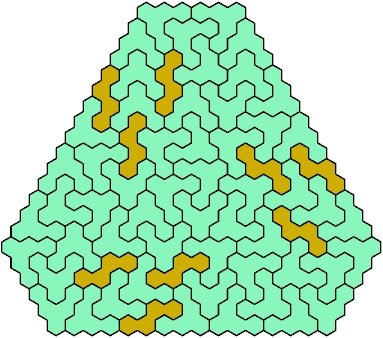
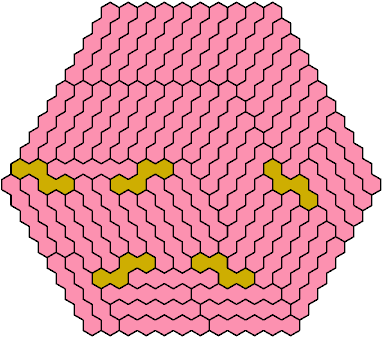
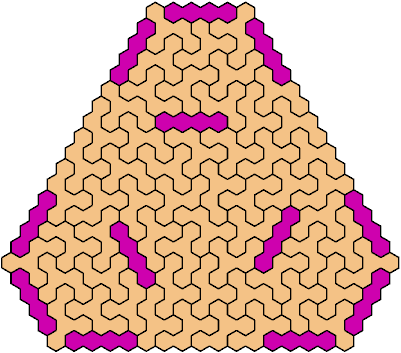
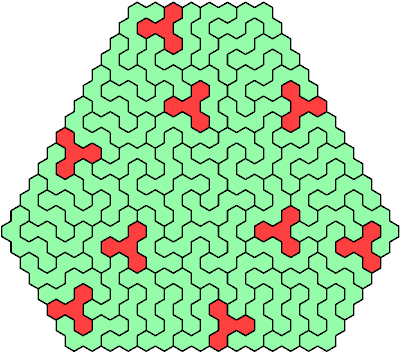
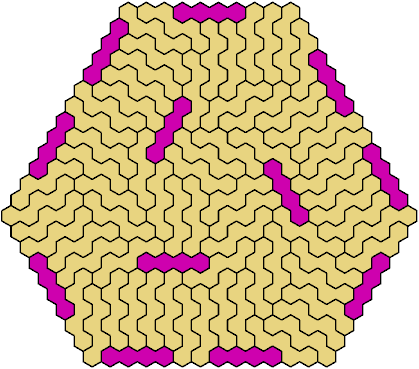
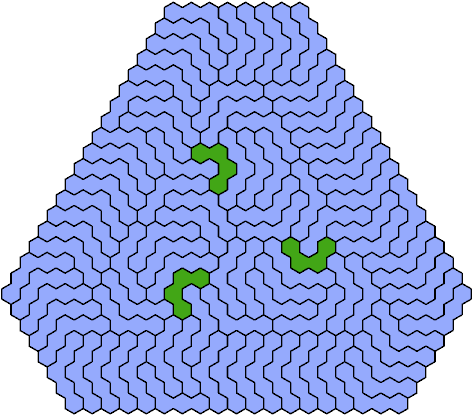
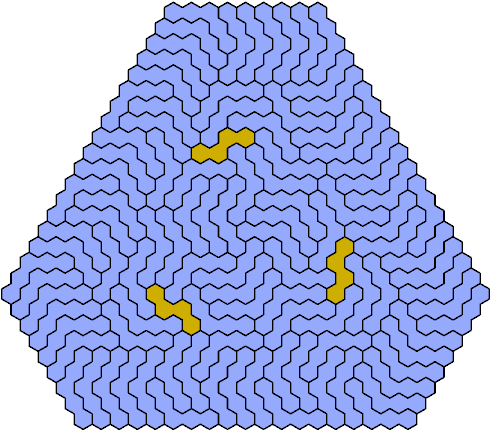
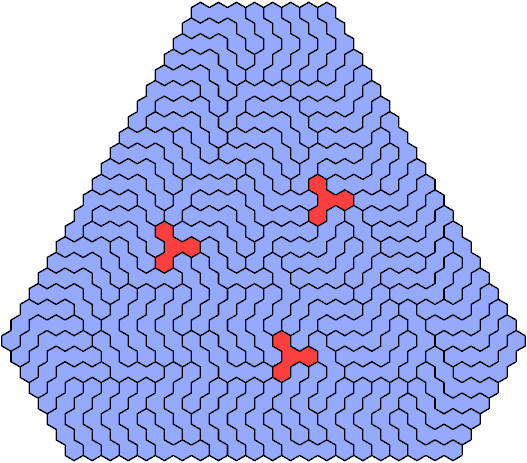
Call a polyhex convex if the region enclosed by joining centers of adjacent cells is convex. A badge is a convex polyhex with 3-rotary symmetry and horizontal mirror symmetry. Here I tile minimal known badges with copies of a pentahex and a tetrahex so that copies of the tetrahex do not touch.
See also
| Pentahex | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
| I | 42 | ? | 27 | 27 | 141 | 333 | 60 | 42 | 42 | 42 | 27 | 42 | 42 | 213 | ? | ? | ? | 73 | 393 | ? | 27 | 42 |
| J | 27 | 27 | 27 | 153 | 27 | 27 | 106 | 27 | 27 | 48 | 27 | 27 | 27 | 27 | 42 | ? | 27 | 57 | 57 | 27 | 42 | 42 |
| O | 27 | 123 | 27 | 66 | ? | ? | 126 | 141 | 27 | 33 | 42 | 27 | 27 | 27 | 27 | ? | ? | 27 | ? | ? | 33 | ? |
| Q | 27 | 144 | 27 | 28 | 27 | 153 | 57 | 27 | 27 | 42 | 27 | 28 | 27 | 60 | 621 | ? | 27 | 57 | 66 | 27 | 42 | 42 |
| S | 306 | ? | 63 | 66 | 87 | ? | 330 | 42 | ? | 87 | 87 | 42 | ? | 636 | ? | ? | 27 | 522 | ? | ? | 73 | ? |
| U | 57 | ? | 57 | 42 | ? | 27 | 147 | 57 | 27 | 73 | 42 | 33 | 42 | 126 | ? | ? | 27 | 477 | ? | 27 | 63 | 201 |
| Y | 645 | ? | 73 | 696 | 351 | ? | ? | ? | ? | 87 | 57 | 57 | ? | ? | ? | ? | ? | 582 | ? | ? | 123 | ? |







Last revised 2025-06-20.