Pentahex Pair Hex-Convex Shapes

Introduction

A polyhex is said to be hex-convex if every line joining the centers of two of its cells lies in its interior. Here are the smallest known hex-convex polyhexes that can be formed with copies of two pentahexes, using at least one of each.

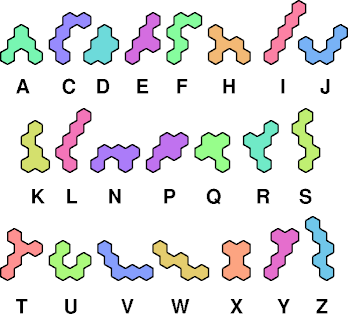
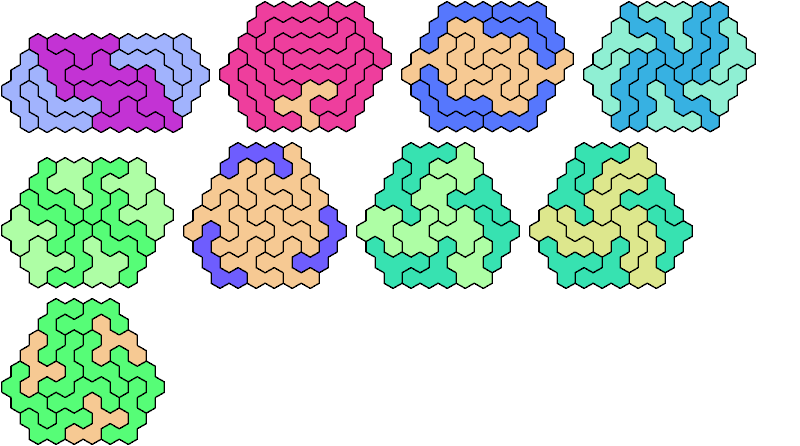
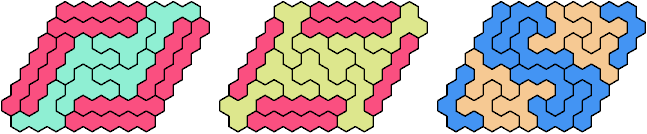
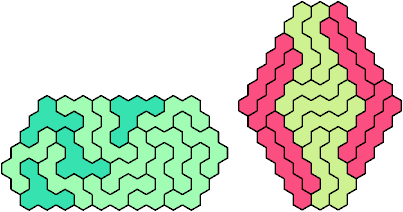
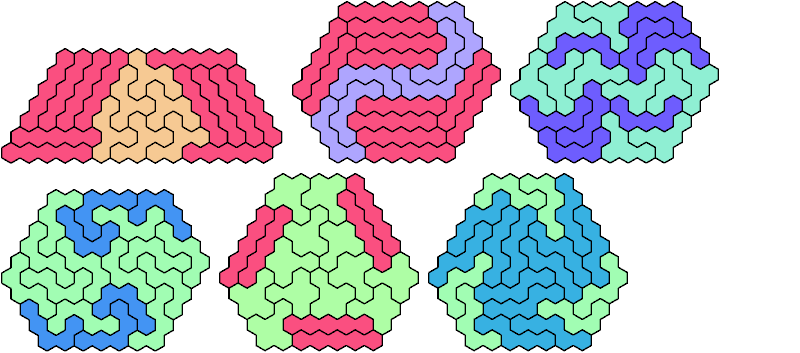
See also Tiling a Hex-Convex Polyhex with a Polyhex.

Nomenclature

Table of Results

 ACDEFHIJKLNPQRSTUVWXYZ
A•632630644433461264246141356
C6•242612181356644618——466—610
D32•3693243334338539328
E2423•4644654364271264126458
F6664•121318206751215———422010418
H30129612•1814—1266—27——812——9—
I618341318•101434318141523856248839
J413524181410•553444—66—6—838
K464620—145•464—12——64——5—
L4635612354•3367810664844
N3434764363•34696969334
P34335634433•4437464534
Q464612—184—644•12——26——4—
R6183415271441276412•——6616141312
S126—327——15——893——•——3——3—
T42—8126——23866—1067———•—29——10—
U4454—85—669426——•6—536
V663124212664666663296•241744
W14169620—24——494—16———24•—6—
X3—3410—888—835—141——517—•5—
Y562549335433433103465•4
Z6108818—98—444—12——64——4•

Navigation

[2 Tiles] [3 Tiles] [4 Tiles] [5 Tiles] [6 Tiles] [7 Tiles] [8 Tiles] [9 Tiles] [10 Tiles] [12 Tiles] [13 Tiles] [14 Tiles] [15 Tiles] [16 Tiles]
[17 Tiles] [18 Tiles] [20 Tiles] [24 Tiles] [27 Tiles] [29 Tiles] [30 Tiles] [42 Tiles] [66 Tiles] [88 Tiles] [126 Tiles] [135 Tiles] [141 Tiles] [238 Tiles]

Solutions

These minimal known solutions are not necessarily unique.

2 Tiles

3 Tiles

4 Tiles

5 Tiles

6 Tiles

7 Tiles

8 Tiles

9 Tiles

10 Tiles

12 Tiles

13 Tiles

14 Tiles

15 Tiles

16 Tiles

17 Tiles

18 Tiles

20 Tiles

24 Tiles

27 Tiles

29 Tiles

30 Tiles

42 Tiles

66 Tiles

88 Tiles

126 Tiles

135 Tiles

141 Tiles

238 Tiles

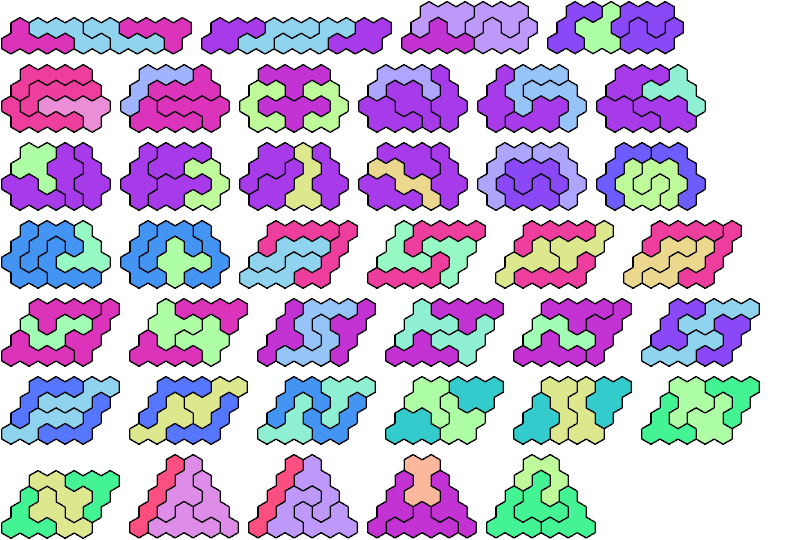
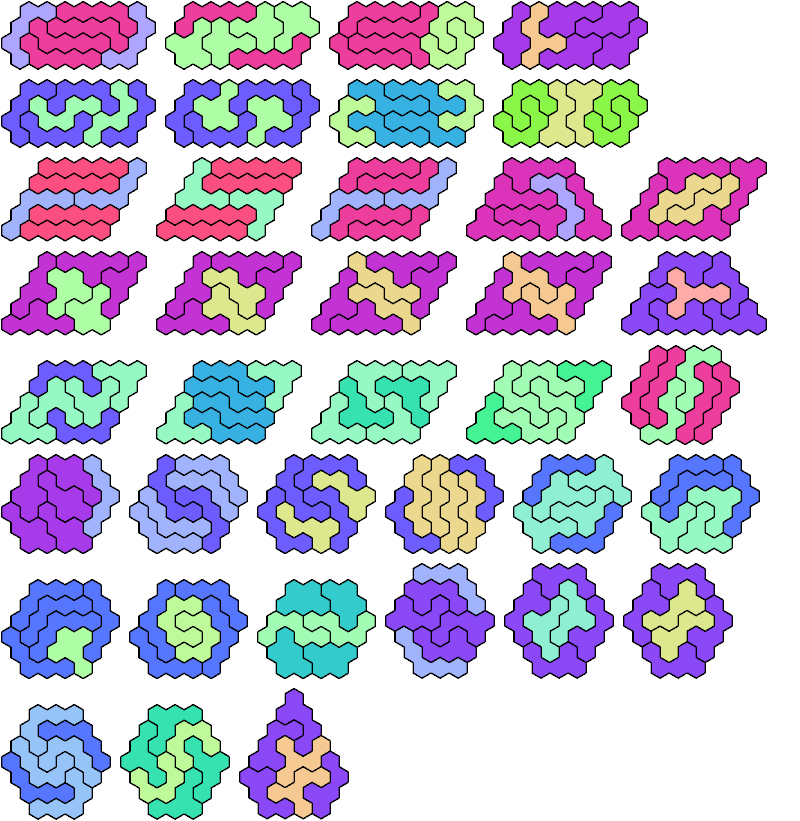
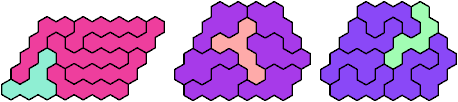
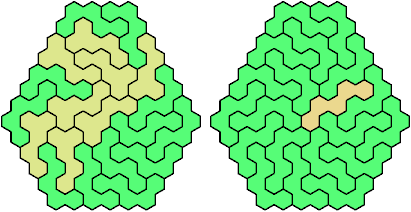
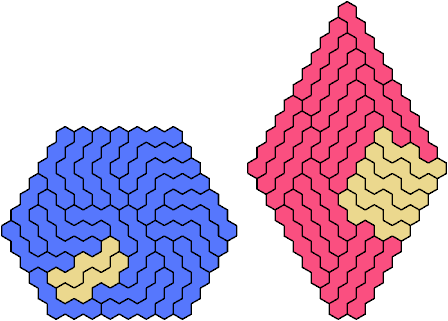
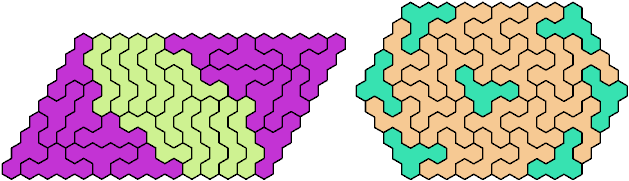
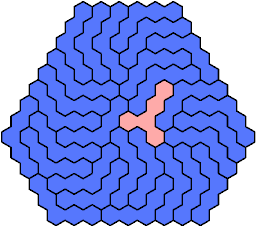
Last revised 2025-08-18.

Back to Polyhex Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]