Here I show the smallest hex-convex polyhex that can be tiled with a given polyhex with from 1 to 7 cells. The minimal tilings shown are not necessarily uniquely minimal. Polyhexes not shown have no known solution.
See also Pentahex Pair Hex-Convex Shapes.




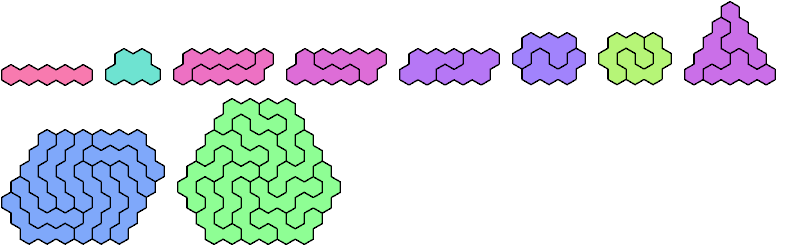

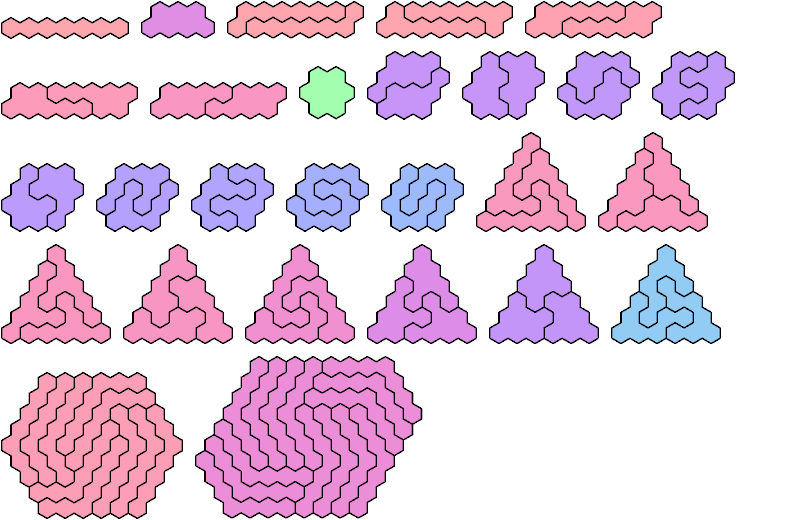
Last revised 2025-08-15.