Baiocchi Figures for Hexiamond-Heptiamond Pairs

Here I show the smallest polyiamond with full symmetry that can be tiled by a hexiamond and a heptiamond, using at least one copy of each. The solutions shown are not necessarily uniquely minimal.

For holeless variants, see Holeless Baiocchi Figures for Hexiamond-Heptiamond Pairs.

See also

In the table, the figures indicate the numbers of polyiamond cells in the solutions.

Carl Schwenke and Johann Schwenke contributed many improvements.

6A+7A : 78	6E+7A : 78	6F+7A : 78	6H+7A : 78	6I+7A : 78	6L+7A : 78
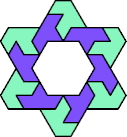6O+7A : 78	6P+7A : 78	6S+7A : 78	6U+7A : 78	6V+7A : 78	6X+7A : 120
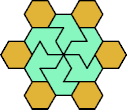6A+7B : 78	6E+7B : 96	6F+7B : 60	6H+7B : 78	6I+7B : 78	6L+7B : 78
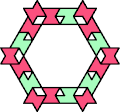
6O+7B : 90	6P+7B : 78	6S+7B : 114	6U+7B : 60	6V+7B : 78	6X+7B : 114
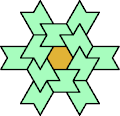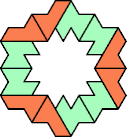6A+7C : 78	6E+7C : 54	6F+7C : 78	6H+7C : 78	6I+7C : 54	6L+7C : 66
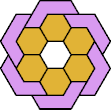
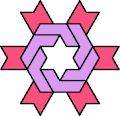
6O+7C : 78	6P+7C : 78	6S+7C : 78	6U+7C : 78	6V+7C : 78	6X+7C : 78
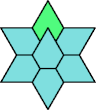
6A+7D : 48	6E+7D : 54	6F+7D : 78	6H+7D : 54	6I+7D : 78	6L+7D : 78
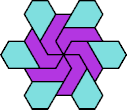6O+7D : 48	6P+7D : 60	6S+7D : 78	6U+7D : 78	6V+7D : 54	6X+7D : 60
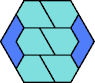6A+7E : 78	6E+7E : 60	6F+7E : 60	6H+7E : 60	6I+7E : 54	6L+7E : 60
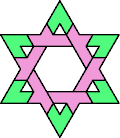6O+7E : 78	6P+7E : 60	6S+7E : 78	6U+7E : 78	6V+7E : 60	6X+7E : 114
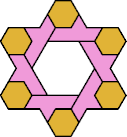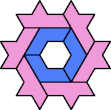6A+7F : 60	6E+7F : 54	6F+7F : 78	6H+7F : 78	6I+7F : 54	6L+7F : 54
6O+7F : 78	6P+7F : 78	6S+7F : 78	6U+7F : 78	6V+7F : 60	6X+7F : 60
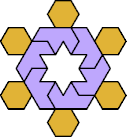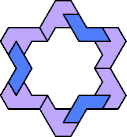6A+7G : 78	6E+7G : 78	6F+7G : 78	6H+7G : 78	6I+7G : 78	6L+7G : 78
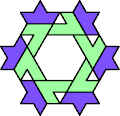6O+7G : 120	6P+7G : 78	6S+7G : 114	6U+7G : 78	6V+7G : 78	6X+7G : 78
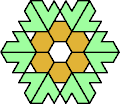6A+7H : 78	6E+7H : 54	6F+7H : 78	6H+7H : 78	6I+7H : 78	6L+7H : 66
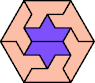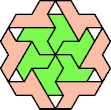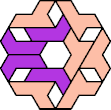6O+7H : 60	6P+7H : 78	6S+7H : 60	6U+7H : 78	6V+7H : 78	6X+7H : 78
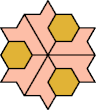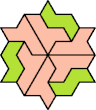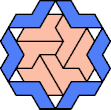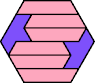
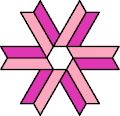
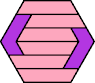
6A+7I : 54	6E+7I : 54	6F+7I : 78	6H+7I : 78	6I+7I : 78	6L+7I : 54
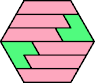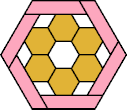
6O+7I : 78	6P+7I : 78	6S+7I : 78	6U+7I : 78	6V+7I : 54	6X+7I : 78
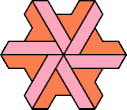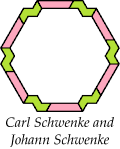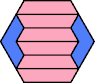6A+7J : 78	6E+7J : 78	6F+7J : 78	6H+7J : 78	6I+7J : 78	6L+7J : 78
6O+7J : 78	6P+7J : 78	6S+7J : 78	6U+7J : 78	6V+7J : 54	6X+7J : 78
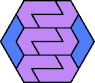6A+7K : 78	6E+7K : 78	6F+7K : 78	6H+7K : 78	6I+7K : 78	6L+7K : 60
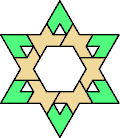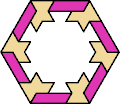6O+7K : 60	6P+7K : 78	6S+7K : 60	6U+7K : 60	6V+7K : 60	6X+7K : 78
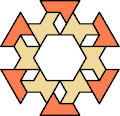6A+7L : 78	6E+7L : 78	6F+7L : 78	6H+7L : 78	6I+7L : 78	6L+7L : 78
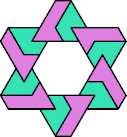6O+7L : 48	6P+7L : 78	6S+7L : 78	6U+7L : 78	6V+7L : 60	6X+7L : 60
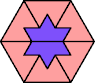
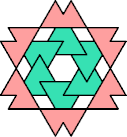
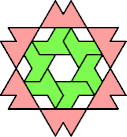
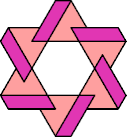
6A+7M : 78	6E+7M : 54	6F+7M : 78	6H+7M : 78	6I+7M : 78	6L+7M : 78
6O+7M : 48	6P+7M : 78	6S+7M : 78	6U+7M : 78	6V+7M : 78	6X+7M : 78
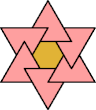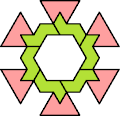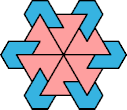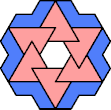6A+7N : 78	6E+7N : 78	6F+7N : 78	6H+7N : 78	6I+7N : 78	6L+7N : 78
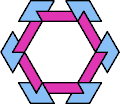6O+7N : 60	6P+7N : 78	6S+7N : 78	6U+7N : 78	6V+7N : 60	6X+7N : 120
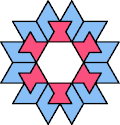6A+7P : 78	6E+7P : 78	6F+7P : 78	6H+7P : 78	6I+7P : 78	6L+7P : 78
6O+7P : 48	6P+7P : 78	6S+7P : 60	6U+7P : 60	6V+7P : 78	6X+7P : 78
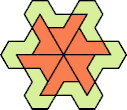6A+7Q : 78	6E+7Q : 96	6F+7Q : 78	6H+7Q : 78	6I+7Q : 78	6L+7Q : 78
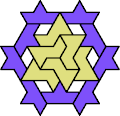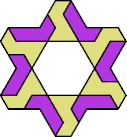6O+7Q : 78	6P+7Q : 78	6S+7Q : 78	6U+7Q : 78	6V+7Q : 60	6X+7Q : 60
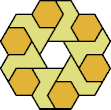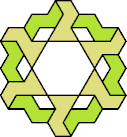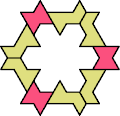6A+7R : 78	6E+7R : 78	6F+7R : 78	6H+7R : 54	6I+7R : 78	6L+7R : 78
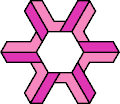6O+7R : 78	6P+7R : 78	6S+7R : 78	6U+7R : 78	6V+7R : 54	6X+7R : 78
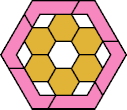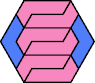6A+7S : 78	6E+7S : 78	6F+7S : 78	6H+7S : 78	6I+7S : 78	6L+7S : 78
6O+7S : 78	6P+7S : 60	6S+7S : 60	6U+7S : 54	6V+7S : 78	6X+7S : 78
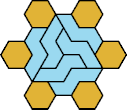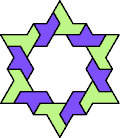
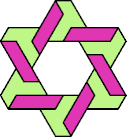
6A+7T : 78	6E+7T : 78	6F+7T : 78	6H+7T : 78	6I+7T : 78	6L+7T : 78
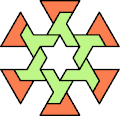
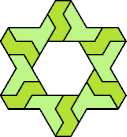
6O+7T : 48	6P+7T : 78	6S+7T : 78	6U+7T : 60	6V+7T : 78	6X+7T : 78
6A+7U : 78	6E+7U : 78	6F+7U : 78	6H+7U : 78	6I+7U : 114	6L+7U : 60
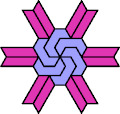6O+7U : 78	6P+7U : 66	6S+7U : 78	6U+7U : 78	6V+7U : 60	6X+7U : 78
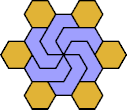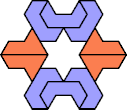6A+7V : 78	6E+7V : 78	6F+7V : 78	6H+7V : 78	6I+7V : 78	6L+7V : 78
6O+7V : 48	6P+7V : 78	6S+7V : 78	6U+7V : 78	6V+7V : 78	6X+7V : 78
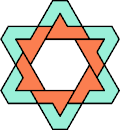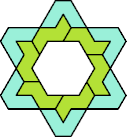6A+7X : 114	6E+7X : 78	6F+7X : 78	6H+7X : 78	6I+7X : 114	6L+7X : 78
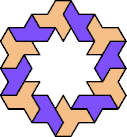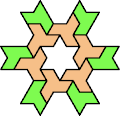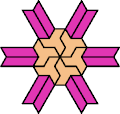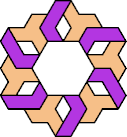6O+7X : 78	6P+7X : 114	6S+7X : 60	6U+7X : 78	6V+7X : 78	6X+7X : 120
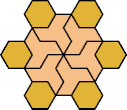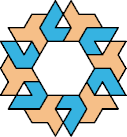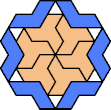6A+7Y : 78	6E+7Y : 54	6F+7Y : 60	6H+7Y : 54	6I+7Y : 78	6L+7Y : 54
6O+7Y : 78	6P+7Y : 54	6S+7Y : 78	6U+7Y : 78	6V+7Y : 78	6X+7Y : 78
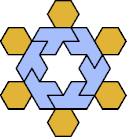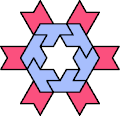6A+7Z : 114	6E+7Z : 96	6F+7Z : 78	6H+7Z : 78	6I+7Z : 114	6L+7Z : 78
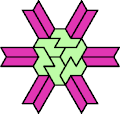6O+7Z : 78	6P+7Z : 78	6S+7Z : 60	6U+7Z : 60	6V+7Z : 60	6X+7Z : 120

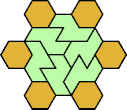Last revised 2025-03-12.