

This page shows minimal known oddities and similar constructions for various polyominoes and polykings, with various symmetries.
[Polyominoes] [Polykings]
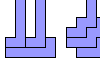 | Polyomino Oddities. Oddities for polyominoes of order up to 7. |
 | Pentomino Oddities. Pentomino oddities with specific symmetries. |
 | One-Sided Pentomino Oddities. One-sided pentomino oddities with specific symmetries. |
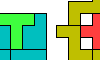 | Pentomino Pair Full Oddities. Full-symmetry polyominoes tiled with an odd number of two different pentominoes. |
 | Pentomino Pair Dual Orthogonal Oddities. Polyominoes with dual orthogonal mirror symmetry tiled with an odd number of two different pentominoes. |
 | Pentomino Pair Dual Diagonal Oddities. Polyominoes with dual diagonal mirror symmetry tiled with an odd number of two different pentominoes. |
 | Pentomino Pair 4-Rotary Oddities. Polyominoes with 4-rotary symmetry tiled with an odd number of two different pentominoes. |
 | Tetromino-Pentomino Pair Oddities. Use copies of a tetromino and a pentomino to form a full-symmetry polyomino with an odd number of cells. |
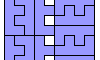 | Hexomino Oddities. Hexomino oddities with specific symmetries. |
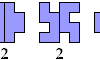 | Polyomino Semi-Oddities. Semi-oddities for polyominoes. A semi-oddity is a figure with quaternary symmetry and an even number of tiles that is not a multiple of 4. |
 | Semi-Oddities for Hexomino Pairs. Full-symmetry semi-oddities formed with copies of two hexominoes. |
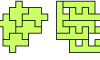 | Heptomino Oddities. Heptomino oddities with specific symmetries. |
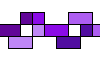 | Triking Oddities. Oddities with specific symmetries for pseudopolyominoes of order 3. |
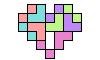 | Pentaking Oddities. Oddities with specific symmetries for pseudopolyominoes of order 5. |