See also

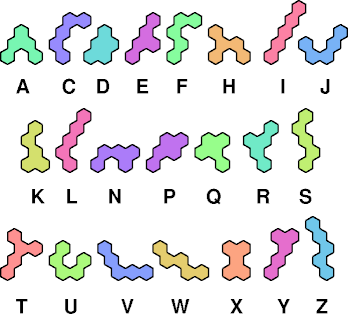
| Isolated Pentahex | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
| A | • | 6 | 3 | 2 | 60 | 66 | 9 | 4 | 54 | 4 | 10 | 10 | 6 | 6 | — | 225 | 4 | 33 | — | 3 | 12 | 9 |
| C | — | • | 2 | — | 16 | — | — | — | 6 | 24 | — | 10 | 6 | — | — | — | — | — | 12 | — | — | — |
| D | 6 | 2 | • | 3 | 9 | 9 | 3 | 2 | 6 | 4 | 3 | 3 | 6 | 3 | 3 | 8 | — | 3 | 9 | 3 | 2 | 8 |
| E | 2 | 48 | 8 | • | 4 | 22 | 4 | 8 | 14 | 8 | 6 | 3 | 9 | 6 | 141 | — | 4 | 74 | 20 | 4 | 10 | 10 |
| F | 6 | — | 13 | 4 | • | 12 | 13 | — | 30 | 15 | 12 | 9 | 14 | 18 | — | — | — | — | 20 | 10 | 12 | 30 |
| H | — | 12 | — | 22 | 33 | • | 46 | 46 | — | 12 | 30 | 14 | — | 27 | — | — | 8 | — | — | — | 15 | — |
| I | 11 | 60 | 3 | 13 | 78 | 84 | • | 18 | 41 | 4 | 6 | 4 | 44 | 33 | 43 | — | 6 | 11 | 66 | — | 4 | 18 |
| J | 4 | — | 2 | 4 | — | — | 15 | • | 6 | 10 | 4 | 6 | 4 | 4 | — | 84 | — | 6 | — | 14 | 4 | 8 |
| K | 4 | 46 | 4 | 20 | 33 | — | 18 | 10 | • | 4 | 18 | 8 | — | 20 | — | — | — | 4 | — | — | 9 | — |
| L | 4 | 6 | 3 | 8 | 7 | 12 | 3 | 5 | 8 | • | 4 | 6 | 7 | 7 | 10 | 10 | 8 | 7 | 11 | 8 | 4 | 6 |
| N | 3 | 6 | 3 | 4 | 7 | 8 | 4 | 3 | 6 | 3 | • | 4 | 4 | 8 | 9 | 6 | 9 | 6 | 9 | 3 | 3 | 8 |
| P | 3 | 4 | 3 | 3 | 5 | 6 | 3 | 4 | 4 | 3 | 3 | • | 4 | 4 | 3 | 7 | 4 | 6 | 4 | 5 | 3 | 6 |
| Q | 4 | 12 | 4 | 15 | 41 | — | 25 | 8 | — | 6 | 6 | 12 | • | 66 | — | — | 2 | 20 | — | — | 4 | — |
| R | 36 | 33 | 3 | 4 | 40 | — | 16 | 8 | — | 20 | 6 | 8 | — | • | — | — | 10 | 6 | — | — | 4 | 72 |
| S | — | — | 3 | — | — | — | — | — | — | — | — | 3 | — | — | • | — | — | 3 | — | — | 3 | — |
| T | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | • | — | — | — | — | — | — |
| U | — | — | — | 6 | — | — | — | — | — | 6 | — | 6 | 2 | 14 | — | — | • | 15 | — | 5 | 3 | — |
| V | 9 | 18 | 6 | 21 | — | 58 | 10 | 10 | 14 | 17 | 8 | 6 | 6 | 18 | 3 | 29 | 118 | • | 84 | 17 | 4 | 15 |
| W | — | 6 | — | 9 | — | — | — | — | — | 4 | — | 8 | — | 30 | — | — | — | — | • | — | 93 | — |
| X | 3 | — | 3 | 20 | 56 | — | — | — | — | — | 3 | 84 | — | — | — | — | — | — | — | • | — | — |
| Y | 7 | 6 | 2 | 8 | 4 | 12 | 3 | 3 | 9 | 4 | 5 | 3 | 7 | 3 | 3 | 10 | 8 | 4 | 7 | 5 | • | 6 |
| Z | 6 | 10 | 14 | 9 | 46 | — | 9 | 8 | — | 4 | 4 | 4 | — | 14 | — | — | 6 | 4 | — | — | 4 | • |
























Last revised 2025-08-26.