

An oddity is a geometric figure with binary symmetry or better, formed by joining an odd number of congruent polyforms.
This page shows minimal known oddities and similar constructions for various polyiamond and polymings with various symmetries.
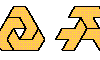 | Pentiamond, Heptiamond, and Enneiamond Oddities. Oddities for pentiamonds, heptiamonds, and enneiamonds. Oddities for polyiamonds of odd order can have only bilateral symmetry. |
 | Hexiamond Oddities. Hexiamond oddities with specific symmetries. |
 | Hexiamond Pair Full Oddities. Full-symmetry polyiamonds tiled with an odd number of two different hexiamonds. |
 | Hexiamond Pair Dual Orthogonal Vertex-Centered Oddities. Polyiamonds with dual orthogonal vertex-centered symmetry, tiled with an odd number of two different hexiamonds. |
 | Hexiamond Pair Dual Orthogonal Edge-Centered Oddities. Polyiamonds with dual orthogonal edge-centered symmetry, tiled with an odd number of two different hexiamonds. |
 | Pentiamond-Hexiamond Oddities. Full-symmetry polyiamonds tiled with an odd number of copies of a pentiamond and a hexiamond. |
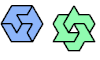 | Octiamond Oddities. Octiamond oddities with specific symmetries. |
 | Polyiamond Tri-Oddities. These are like oddities but with ternary symmetry, for orders 1–6. |
 | Hexiamond Pair Tri-Oddities. Tri-oddities formed with copies of two hexiamonds. |
 | Heptiamond Tri-Oddities. These are like oddities but with ternary symmetry, for order 7. |
 | Tri-Oddities for Heptiamond Pairs. Arrange copies of two heptiamonds to form a figure with ternary symmetry, with the tile count not a multiple of 3. |
 | Horizontally Symmetric Tri-Oddities for Heptiamond Pairs. Arrange copies of two heptiamonds to form a figure with ternary symmetry and horizontal mirror symmetry, with the tile count not a multiple of 3. |
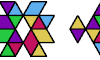 | Tetraming Oddities. Oddities for tetramings, or corner-connected tetriamonds. |